
 ,
,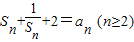 ,通过计算S1,S2,S3,S4,归纳出Sn的表达式
,通过计算S1,S2,S3,S4,归纳出Sn的表达式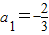 ,
, ,通过计算S1,S2,S3,S4,归纳出Sn的表达式”是归纳推理.故错.
,通过计算S1,S2,S3,S4,归纳出Sn的表达式”是归纳推理.故错.

科目:高中数学 来源: 题型:
| A、某校高三1班有55人,2班有54人,3班有52人,由此得高三所有班人数超过50人 | ||||
| B、两条直线平行,同旁内角互补,如果∠A与∠B是两条平行直线的同旁内角,则∠A+∠B=180° | ||||
| C、由平面三角形的性质,推测空间四面体性质 | ||||
D、在数列{an}中a1=1,an=
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、两条直线平行,同旁内角互补,如果∠A与∠B是两条平行直线的同旁内角,则∠A+∠B=180° | ||||
| B、某校高二(1)班有55人,高二(2)班有52人,由此得高二所有班人数超过50人 | ||||
| C、由平面三角形的性质,推出空间四边形的性质 | ||||
D、在数列{an}中,a1=1,an=
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.在数列{an}中a1=1,an=
| ||||
| B.大足中学高一一班有63人,二班65人,三班62人,由此得高一所有班人数都超过60人. | ||||
| C.两条直线平行,内错角相等,如果∠A与∠B是两条平行直线的内错角,则∠A=∠B. | ||||
| D.由平面内正三角形的性质,推知空间正四面体的性质. |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年重庆市大足中学高二(下)第三次月考数学试卷(理科)(解析版) 题型:选择题
 ,由此得出{an}的通项公式.
,由此得出{an}的通项公式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com