
【题目】设函数![]() .
.
(1)试说明![]() 的图象由函数
的图象由函数![]() 的图象经过怎样的变化得到?并求
的图象经过怎样的变化得到?并求![]() 的单调区间;
的单调区间;
(2)若函数![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称,当
对称,当![]() 时,求函数
时,求函数![]() 的最值.
的最值.
【答案】(1)见解析(2)最小值为﹣1;最大值为![]()
【解析】试题分析:(1)利用三角恒等变换化简![]() 的解析式,再利用函数
的解析式,再利用函数![]() 的图象变换规律,得出结论.
的图象变换规律,得出结论.
(2)先根据对称性求得![]() 的解析式,再利用正弦函数的定义域和值域,求得当
的解析式,再利用正弦函数的定义域和值域,求得当![]() ]时,函数
]时,函数![]() 的最值.
的最值.
试题解析:(1)∵函数![]() =sin
=sin![]() xcos
xcos![]() ﹣cos
﹣cos![]() xsin
xsin![]() ﹣cos
﹣cos![]() x﹣1=
x﹣1=![]() sin
sin![]() x﹣
x﹣![]() cos
cos![]() ﹣1=
﹣1=![]() sin(
sin(![]() x﹣
x﹣![]() )﹣1,
)﹣1,
故把函数![]() 的图象向右平移1个单位,可得y=
的图象向右平移1个单位,可得y=![]() sin(
sin(![]() x﹣
x﹣![]() )的图象;
)的图象;
再向下平移1个单位,可得f(x)的图象.
(2)函数y=g(x)与y=f(x)的图象关于直线x=2对称,∴g(x)=f(4﹣x)=![]() sin[
sin[![]() (4﹣x)﹣
(4﹣x)﹣![]() ]﹣1=sin(
]﹣1=sin(![]() x)﹣1,
x)﹣1,
当x∈[0,1]时,![]() x∈[0,
x∈[0,![]() ],故当x=0时,函数y=g(x)取得最小值为﹣1;当x=1时,函数y=g(x)取得最大值为
],故当x=0时,函数y=g(x)取得最小值为﹣1;当x=1时,函数y=g(x)取得最大值为![]() ﹣1.
﹣1.


科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1 , D1C1上,A1E=D1F=4.过E,F的平面α与此长方体的面相交,交线围成一个正方形 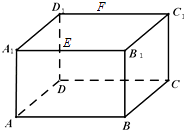
(1)在图中画出这个正方形(不必说出画法和理由)
(2)求平面α把该长方体分成的两部分体积的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2008年至2016年粮食产量的部分数据如下表:

(1)求该地区2008年至2016年的粮食年产量![]() 与年份
与年份![]() 之间的线性回归方程;
之间的线性回归方程;
(2)利用(1)中的回归方程,分析2008年至2016年该地区粮食产量的变化情况,并预测该地区 2018年的粮食产量.
附:回归直线的斜率和截距的最小二乘估计公式分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,M、N分别是棱AA1、AD的中点,设E是棱AB的中点. 
(1)求证:MN∥平面CEC1;
(2)求平面D1EC1与平面ABCD所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将参加数学竞赛的1000名学生编号如下:0001,0002,003,…,1000,打算从中抽取一个容量为50的样本,按系统抽样的方法把编号分成50个部分,如果第一部分编号为0001,0002,0003,…,0020,第一部分随机抽取一个号码为0013,那么抽取的第40个号码 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com