
【题目】已知无穷等比数列![]() 的首项、公比均为
的首项、公比均为![]() .
.
(1)试求无穷等比子数列![]() 各项的和;
各项的和;
(2)是否存在数列![]() 的一个无穷等比子数列,使得它各项的和为
的一个无穷等比子数列,使得它各项的和为![]() ?若存在,求出所有满足条件的子数列的通项公式;若不存在,请说明理由.
?若存在,求出所有满足条件的子数列的通项公式;若不存在,请说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,AB=1,BC=2,AC![]() ,PC
,PC![]() ,PA
,PA![]() ,PB
,PB![]() ,E是线段BC的中点.
,E是线段BC的中点.
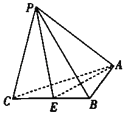
(1)求点C到平面APE的距离d;
(2)求二面角P﹣EA﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,ABCD为梯形,AB//CD,BC⊥AB,AB=2![]() ,BC=
,BC=![]() ,CD=PC=
,CD=PC=![]() 。
。
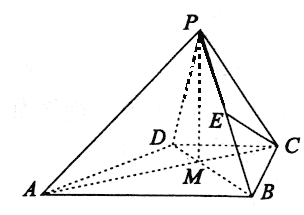
(I)点E在线段PB上,满足CE//平面PAD,求![]() 的值。
的值。
(II)已知AC与BD的交点为M,若PM=1,且平面PAC⊥平面ABCD,求二面角P-BC-M平面角的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
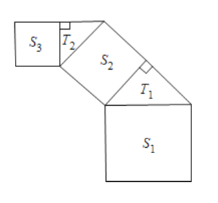
【题目】如图所示,正方形上连接等腰直角三角形,直角三角形上再连接正方形……如此无限重复下去,设正方形面积为![]() ,三角形面积为
,三角形面积为![]() .当第一个正方形的边长为2时,则这些正方形和三角形的面积的总和为______.
.当第一个正方形的边长为2时,则这些正方形和三角形的面积的总和为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,已知
,已知![]() 是边长为6的等边三角形,点D、E分别是边AB、AC上的点,且满足
是边长为6的等边三角形,点D、E分别是边AB、AC上的点,且满足![]() ,如图
,如图![]() ,将
,将![]() 沿DE折成四棱锥
沿DE折成四棱锥![]() ,且有平面
,且有平面![]() 平面BCED.
平面BCED.

![]() 求证:
求证:![]() 平面BCED;
平面BCED;
![]() 记
记![]() 的中点为M,求二面角
的中点为M,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() (
(![]() ),
),![]() (
(![]() ),则下列说法中错误的是( )
),则下列说法中错误的是( )
A.若![]() ,则数列
,则数列![]() 为递增数列
为递增数列
B.若数列![]() 为递增数列,则
为递增数列,则![]()
C.存在实数![]() ,使数列
,使数列![]() 为常数数列
为常数数列
D.存在实数![]() ,使
,使![]() 恒成立
恒成立
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com