
����Ŀ��һ�����̾����һ������OPQ��Ƥ����Բ�Ľǡ�POQ= ![]() ���뾶ΪR=200m�����������ڴ˵�Ƥ����һ��ƽ��ͼΪ���ε���ס¥��Ϊʹ�õ�Ƥ��ʹ�����������������Ʒ�����ͼ������һ������ABCD��һ��AB�ڰ뾶OP�ϣ�C��Բ���ϣ�D�ڰ뾶OQ��������������EFGH�Ķ�����Բ���ϣ�����G��H�ֱ��������뾶�ϣ�����ͨ�����㣬Ϊ�������ṩ���߽��飮
���뾶ΪR=200m�����������ڴ˵�Ƥ����һ��ƽ��ͼΪ���ε���ס¥��Ϊʹ�õ�Ƥ��ʹ�����������������Ʒ�����ͼ������һ������ABCD��һ��AB�ڰ뾶OP�ϣ�C��Բ���ϣ�D�ڰ뾶OQ��������������EFGH�Ķ�����Բ���ϣ�����G��H�ֱ��������뾶�ϣ�����ͨ�����㣬Ϊ�������ṩ���߽��飮 
���𰸡��⣺������һ����ͼ����OC���� ![]() ��
�� 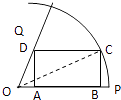
��Rt��OBC��BC=Rsinx��OB=Rcosx����DA=Rsinx
��Rt��OAD�� ![]() ����
���� ![]() ��
��
�� 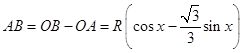 �������ABCD�����Ϊy����
�������ABCD�����Ϊy����
y=ABBC= 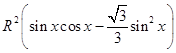 =
= ![]() sin��2x+
sin��2x+ ![]() ����
���� ![]() ��
��
�� ![]() ��
�� ![]() ��
��
���Ե� ![]() ����
���� ![]() ʱ
ʱ 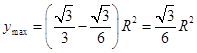 ��
��
������������ͼ����POQ��ƽ���߷ֱ�EF��GH�ڵ�M��N����OE��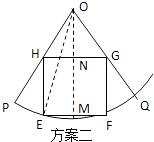
�� ![]() ����Rt��MOE��ME=Rsin����OM=Rcos��
����Rt��MOE��ME=Rsin����OM=Rcos��
��Rt��ONH�� ![]() ����
���� ![]() ��
��
�� ![]() �������EFGH�����ΪS��
�������EFGH�����ΪS��
��S=2MEMN=2R2sin����cos���� ![]() sin����=R2��sin2��+
sin����=R2��sin2��+ ![]() cos2����
cos2���� ![]() ��=
��= ![]()
�� ![]() ����
���� ![]() �����Ե�
�����Ե� ![]() ����
���� ![]() ʱ
ʱ ![]() ��
�� ![]() ����ymax��Smax
����ymax��Smax
�𣺸�������������߽��飺ѡ�÷���һ���ã�
���������������ۣ����շ���һ������Ҫ��������ۣ�
����һ����OC���� ![]() �������ABCD�����Ϊy����y=ABBC��ͨ�����뻯�������Ǻ�������ֵȷ�������������Եó��𰸣�������������POQ��ƽ���߷ֱ�EF��GH�ڵ�M��N����OE����
�������ABCD�����Ϊy����y=ABBC��ͨ�����뻯�������Ǻ�������ֵȷ�������������Եó��𰸣�������������POQ��ƽ���߷ֱ�EF��GH�ڵ�M��N����OE���� ![]() �������EFGH�����ΪS�����S��ʽ�ӣ������Ǻ��������������ֵ��
�������EFGH�����ΪS�����S��ʽ�ӣ������Ǻ��������������ֵ��
��Ƚ϶������ֵ�Ĵ�С��ѡ�����ֵ���ɵó��𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
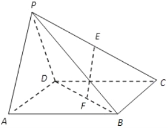
����Ŀ�������������ε�������![]() �У�����
������![]() ����
����![]() ����
����![]() �ǵ���ֱ�������Σ�����
�ǵ���ֱ�������Σ�����![]() ��
��![]() �ֱ�Ϊ�߶�
�ֱ�Ϊ�߶�![]() ���е㣬�����߶�
���е㣬�����߶�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ�ö����
��ʹ�ö����![]() ������ֵΪ
������ֵΪ![]() �������ڣ��������
�������ڣ��������![]() ��λ�ã��������ڣ���˵������.
��λ�ã��������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������f(x)��tx2��(22t��60)x��144t(x��0)��
(1)Ҫʹf(x)��0���������t����Сֵ��
(2)��f(x)��0����ʹt��20������x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������ӣ�ÿ�����Ӷ�װ��4����ȫ��ͬ��С�����Ϸֱ��������1,2,3,4.
(1)�״�����һ������������һ�����Ҵ���һ����������һ����˭���������ϱ�����ִ�˭�ͻ�ʤ����������ͬ��Ϊƽ�֣������ʤ�ĸ��ʣ�
(2)�����루1��ͬ�����涨��������������������������ͬ��ʤ���������ֲ���ͬ���һ�ʤ�������涨��ƽ����˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����¼�![]() ��ʾ������
��ʾ������![]() �ķ���
�ķ���![]() ��ʵ��������
��ʵ��������
��1����![]() ��
��![]() �����¼�
�����¼�![]() �����ĸ���
�����ĸ���![]() ��
��
��2����![]() ��
��![]() �����¼�
�����¼�![]() �����ĸ���
�����ĸ���![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ʱ������
ʱ������![]() �ĵ��������뼫ֵ��
�ĵ��������뼫ֵ��
��2����![]() ������
������![]() �IJ���ʽ
�IJ���ʽ![]() ���������
���������![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ⱥ�и���Ѫ�͵�����ռ�ı������£�
Ѫ�� | A | B | AB | O |
��Ѫ�͵�����ռ����(%) | 28 | 29 | 8 | 35 |
��֪ͬ��Ѫ�͵��˿�����Ѫ��O��Ѫ��������κ�һ��Ѫ�͵��ˣ�������ͬѪ�͵��˲��ܻ�����Ѫ��С����B��Ѫ����С������Ҫ��Ѫ���ʣ�
(1)����һ���ˣ���Ѫ�������С���ĸ����Ƕ��٣�
(2)����һ���ˣ���Ѫ�������С���ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�۲�վ�ڸۿ�A����ƫ��40�㷽���C�������һ���ھ�۲�վ31�����B���������ŴӸۿڳ�����һ����ƫ��20��ĺ�������ۿ�A��ȥ����������20���ﵽ��D������ʱ�۲�վ�ֲ��CD����21����ʴ�ʱ����ۿ�A�����ж�Զ�� 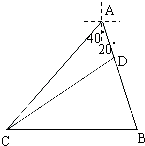
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ҵ繫˾���۲��Ź���200λ����Ա��ÿλ���Ŷ�ÿλ����Ա����1400��Ԫ���������������֪��200λ����Աȥ��������۶������![]() ����λ������Ԫ���ڣ��ֽ���ֳ�5�飬��1�飬��2�飬��3�飬��4�飬��5���Ӧ������ֱ�Ϊ
����λ������Ԫ���ڣ��ֽ���ֳ�5�飬��1�飬��2�飬��3�飬��4�飬��5���Ӧ������ֱ�Ϊ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() �����Ƴ�Ƶ�ʷֲ�ֱ��ͼ.
�����Ƴ�Ƶ�ʷֲ�ֱ��ͼ.

��1����![]() ��ֵ�������������������������
��ֵ�������������������������
��2���÷ֲ��������200λ����Ա�г�ȡ����Ϊ25������������5��ֱ�Ӧ��ȡ��������
��3���ִӣ�2�������������������Ա�����ѡȡ2λ�������������������Σ����ô˽�����2λ����Ա��ͬһ��ĸ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com