练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如下图，在Rt△ABC中，∠B=90°，tanC=,AB=a,在△ABC内作一系列的正方形，求所有这些正方形的面积和S.

    解析：设第n个正方形的边长为an，则由三角形相似，可得(其中An=a1+a2+…+an).

    因为AB=a，tanC=，所以BC=2a.于是=，即An=2a-2an.

    当n≥2时，有an=An-An-1=-2an+2an-1，即3an=2an-1,∴.

    因为tanC=，所以AB=a=a1+a1.所以a12=a2.

    所以数列{an2}是首项为a2，公比为的无穷等比数列，

    S=（S1+S2+…+Sn）

    =a2.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2007年普通高等学校招生全国统一考试、数学(北京卷) 题型：044

    如下图，在Rt△AOB中，，斜边AB＝4．Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到，且二面角B－AO－C的直二面角．D是AB的中点．

    ()求证：平面COD⊥平面AOB；

    ()求异面直线AO与CD所成角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    (2007北京，16)如下图，在Rt△AOB中，∠OAB=，斜边AB=4，Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到，且二面角B－AO－C是直二面角．动点D在斜边AB上．

    (1)求证：平面COD⊥平面AOB；

    (2)当D为AB的中点时，求异面直线AO与CD所成角的大小；

    (3)求CD与平面AOB所成角的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在如下图所示的Rt△ABC中，∠A=30°，过直角顶点C在∠ACB内任作一条射线交线段AB于M，则使AM＞AC的概率是（    ）

    A.                   B.                  C.                D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如下图，在Rt△ABC中，∠CAB=90°，|AB|=2,|AC|=,一曲线E过C点，动点P在曲线E上运动，且保持|PA|+|PB|的值不变.

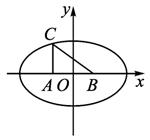
    (1)建立适当的坐标系，求曲线E的方程;

    (2)设点K是曲线E上的一动点，求线段KA中点的轨迹方程;

    (3)若F(1,)是曲线E上的一点，设M、N是曲线E上不同的两点，直线FM和FN的倾斜角互补，试判断直线MN的斜率是否为定值?如果是，求出这个定值;如果不是，请说明理由.

    查看答案和解析>>

    同步练习册答案