
【题目】如图,已知四棱锥![]() 中,底面
中,底面![]() 是正方形,侧面
是正方形,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 上,且
上,且![]() .
.
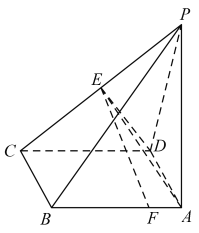
(1)求证:![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)过![]() 作
作![]() 于
于![]() ,连结
,连结![]() ,根据
,根据![]() ,
,![]() ,
,![]() 是
是![]() 的中点,利用平面几何的知识,得到
的中点,利用平面几何的知识,得到![]() ,再结合
,再结合![]() ,即
,即![]() ,得到
,得到![]() ,利用线面垂直的判定定理得到
,利用线面垂直的判定定理得到![]() 面
面![]() 即可.
即可.
(2)由(1)知,![]() 平面
平面![]() ,将点
,将点![]() 到平面
到平面![]() 的距离转化为点
的距离转化为点![]() 到平面
到平面![]() 的距离,根据侧面
的距离,根据侧面![]() 底面
底面![]() ,得到
,得到![]() 侧面
侧面![]() ,设点
,设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,利用等体积法由
,利用等体积法由![]() 求解.
求解.
(1)如图所示:

过![]() 作
作![]() 于
于![]() ,连结
,连结![]() ,
,
因为![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,
所以![]() ,
,
所以![]() ,
,
∵底面![]() 是正方形,
是正方形,![]() ,即
,即![]() ,
,
∴![]() 是矩形,
是矩形,
∴![]() ,
,
又![]() ,
,![]() ,
,
∴![]() 面
面![]() ,
,
又∵![]() 面
面![]() ,
,
∴![]() .
.
(2)由(1)知,![]() 平面
平面![]() ,
,
∴点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,
的距离,
∵底面![]() 是正方形,侧面
是正方形,侧面![]() 底面
底面![]() ,
,
∴![]() 侧面
侧面![]() ,
,
∴![]() ,
,
在三棱锥![]() 中,设点
中,设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
由于![]() ,
,
∴![]() ,
,
在侧面![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 中点,
中点,
∴![]() ,
,![]() ,
,
![]()
∴![]() ,
,
∴![]() ,
,
即点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.


科目:高中数学 来源: 题型:
【题目】观察不等式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 由此归纳第
由此归纳第![]() 个不等式为____________;要用数学归纳法证明该不等式,由
个不等式为____________;要用数学归纳法证明该不等式,由![]() 时不等式成立,推证
时不等式成立,推证![]() 时,左边应增加的项数为____________.
时,左边应增加的项数为____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的首项
的首项![]() (
(![]() 是常数,且
是常数,且![]() ),
),![]()
![]() ,数列
,数列![]() 的首项
的首项![]() ,
,![]()
![]() .
.
(1)证明:![]() 从第2项起是以2为公比的等比数列;
从第2项起是以2为公比的等比数列;
(2)设![]() 为数列
为数列![]() 的前
的前![]() 项和,且
项和,且![]() 是等比数列,求实数
是等比数列,求实数![]() 的值;
的值;
(3)当![]() 时,求数列
时,求数列![]() 的最小项.
的最小项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点P为
,点P为![]() 的中点,
的中点,![]() 交
交![]() 于点D,现将
于点D,现将![]() 沿
沿![]() 翻折至
翻折至![]() ,使得平面
,使得平面![]() 平面
平面![]() .
.
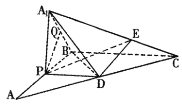
(1)若Q为线段![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点E,使得二面角
上是否存在点E,使得二面角![]() 大小为
大小为![]() .若存在,请求出点E所在位置,若不存在,请说明理由.
.若存在,请求出点E所在位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在气象台![]() 正南方向
正南方向![]() 处有一台风中心,它以
处有一台风中心,它以![]() 的速度向北偏东
的速度向北偏东![]() 方向移动,距台风中心
方向移动,距台风中心![]() 以内的地方都要受其影响.问:从现在起,大约多长时间后,气象台
以内的地方都要受其影响.问:从现在起,大约多长时间后,气象台![]() 所在地将遭受台风影响?持续多长时间?(
所在地将遭受台风影响?持续多长时间?(![]() ,
,![]() ,结果精确到0.01)
,结果精确到0.01)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了判断英语词汇量与阅读水平是否相互独立,某语言培训机构随机抽取了100位英语学习者进行调查,经过计算![]() 的观测值为7,根据这一数据分析,下列说法正确的是( )
的观测值为7,根据这一数据分析,下列说法正确的是( )
附:
| 0.050 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
A.有99%以上的把握认为英语词汇量与阅读水平无关
B.有99.5%以上的把握认为英语词汇量与阅读水平有关
C.有99.9%以上的把握认为英语词汇量与阅读水平有关
D.在犯错误的概率不超过1%的前提下,可以认为英语词汇量与阅读水平有关
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com