
分析 观察已知式子的规律,并改写形式,归纳可得N(n,k)=$\frac{k-2}{2}$n2+$\frac{4-k}{2}$,把n=10,k=24代入可得答案
解答 解:原已知式子可化为:
N(n,3)=$\frac{1}{2}{n}^{2}+\frac{1}{2}n=\frac{3-2}{2}{n}^{2}+\frac{4-3}{2}n$,
N(n,4)=n2=$\frac{4-2}{2}{n}^{2}+\frac{4-4}{2}n$,
N(n,5)=$\frac{3}{2}{n}^{2}-\frac{1}{2}n$=$\frac{5-2}{2}{n}^{2}+\frac{4-5}{2}n$,
N(n,6)=2n2-n=$\frac{6-2}{2}{n}^{2}+\frac{4-6}{2}n$,
由归纳推理可得:
N(n,k)=$\frac{k-2}{2}$n2+$\frac{4-k}{2}$,
故N(10,24)=$\frac{24-2}{2}×1{0}^{2}+\frac{4-24}{2}×10$=1100-100=1000.
故答案为:1000.
点评 本题考查归纳推理,观察已知式子的规律并改写形式是解决问题的关键,是中档题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:选择题
| A. | (4,$\frac{2}{3}$π) | B. | (-4,$\frac{2}{3}$π) | C. | (-4,$\frac{1}{3}$π) | D. | (4,$\frac{1}{3}$π) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 原点对称 | B. | x轴对称 | C. | y轴对称 | D. | 直线y=x对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
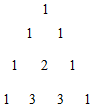 已知杨辉三角,将第4行的第一个数乘以1,第2个数乘以2,第3个数乘以4,第4个数乘以8后,这一行所以所有数字之和等于27(用数字作答):若等比数列{an}的前项是a1,公比是q(q≠1),将杨辉三角的第n+1行的第1个数乘以a1,第2个数乘以a2,…,第n+1个数乘以an+1后,这一行所有数字之和等于a1(1+q)n(用a1,q.n表示)
已知杨辉三角,将第4行的第一个数乘以1,第2个数乘以2,第3个数乘以4,第4个数乘以8后,这一行所以所有数字之和等于27(用数字作答):若等比数列{an}的前项是a1,公比是q(q≠1),将杨辉三角的第n+1行的第1个数乘以a1,第2个数乘以a2,…,第n+1个数乘以an+1后,这一行所有数字之和等于a1(1+q)n(用a1,q.n表示)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
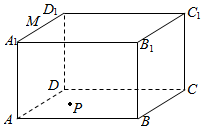 如图,长方体ABCD-A1B1C1D1,AB=BC=2,AA1=$\sqrt{3}$,M为A1D1的中点,P为底面四边形ABCD内的动点,且满足PM=PC,则点P的轨迹的长度为( )
如图,长方体ABCD-A1B1C1D1,AB=BC=2,AA1=$\sqrt{3}$,M为A1D1的中点,P为底面四边形ABCD内的动点,且满足PM=PC,则点P的轨迹的长度为( )| A. | $\sqrt{3}$ | B. | 3 | C. | $\frac{2π}{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com