
【题目】某乐队参加一户外音乐节,准备从3首原创新曲和5首经典歌曲中随机选择4首进行演唱.
(1)求该乐队至少演唱1首原创新曲的概率;
(2)假定演唱一首原创新曲观众与乐队的互动指数为a(a为常数),演唱一首经典歌曲观众与乐队的互动指数为2a.求观众与乐队的互动指数之和 ![]() 的概率分布及数学期望.
的概率分布及数学期望.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aln(x+2)﹣x2在(0,1)内任取两个实数p,q,且p>q,若不等式 ![]() 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A.(﹣∞,24]
B.(﹣∞,12]
C.[12,+∞)
D.[24,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线y2=2px(p>0)的焦点为F,准线为l,A,B是抛物线上的两个动点,且满足∠AFB= ![]() .设线段AB的中点M在l上的投影为N,则
.设线段AB的中点M在l上的投影为N,则 ![]() 的最大值是( )
的最大值是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆中心在坐标原点,A(2,0),B(0,1)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.
(Ⅰ)若 ![]() ,求k的值;
,求k的值;
(Ⅱ)求四边形AEBF面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,已知椭圆
中,已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,C为椭圆上位于第一象限内的一点.
,C为椭圆上位于第一象限内的一点.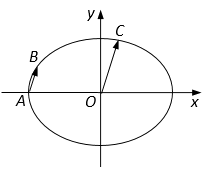
(1)若点 ![]() 的坐标为
的坐标为 ![]() ,求a,b的值;
,求a,b的值;
(2)设A为椭圆的左顶点,B为椭圆上一点,且 ![]() ,求直线AB的斜率.
,求直线AB的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,a,b,c分别为角A,B,C的对边,csinC﹣asinA=( ![]() c﹣b)sinB.
c﹣b)sinB.
(Ⅰ)求角A;
(Ⅱ)若a=1,求三角形ABC面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于下列四个命题
p1:x0∈(0,+∞),( ![]() )x0<(
)x0<( ![]() )x0
)x0
p2:x0∈(0,1), ![]() x0>
x0> ![]() x0
x0
p3:x∈(0,+∞),( ![]() )x>
)x> ![]() x
x
p4:x∈(0, ![]() ),(
),( ![]() )x<
)x< ![]() x.
x.
其中的真命题是( )
A.p1 , p3
B.p1 , p4
C.p2 , p3
D.p2 , p4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)函数f(x)在区间(0,+∞)上是增函数还是减函数?证明你的结论;
(2)当x>0时, ![]() 恒成立,求整数k的最大值;
恒成立,求整数k的最大值;
(3)试证明:(1+12)(1+23)(1+34)…(1+n(n+1))>e2n﹣3 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+ax+b(a,b∈R)在x=ln2处的切线方程为y=x﹣2ln2. (Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若k为差数,当x>0时,(k﹣x)f'(x)<x+1恒成立,求k的最大值(其中f'(x)为f(x)的导函数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com