
| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | -2$\sqrt{2}$ | D. | -2$\sqrt{3}$ |
分析 由任意角的三角函数的定义,根据$cosα=\frac{x}{{\sqrt{{x^2}+{2^2}}}}=-\frac{{\sqrt{3}}}{2}$,求出P点的横坐标.
解答 解:由三角函数定义可得$cosα=\frac{x}{{\sqrt{{x^2}+{2^2}}}}=-\frac{{\sqrt{3}}}{2}$,两边同时平时平方得:$\frac{x^2}{{{x^2}+4}}=\frac{3}{4}$,
解得$x=-2\sqrt{3}$或$x=2\sqrt{3}$,
又因为$cosα=-\frac{{\sqrt{3}}}{2}<0$,所以$x=-2\sqrt{3}$,
故选:D.
点评 本题主要考查任意角的三角函数的定义,考查学生的计算能力,属于基础题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{5}$ | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
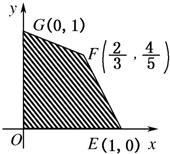 如图,目标函数z=kx-y的可行域为四边形OEFG(含边界),若点F($\frac{2}{3}$,$\frac{4}{5}$)是目标函数的最优解,则k的取值范围是( )
如图,目标函数z=kx-y的可行域为四边形OEFG(含边界),若点F($\frac{2}{3}$,$\frac{4}{5}$)是目标函数的最优解,则k的取值范围是( )| A. | (-$\frac{12}{5}$,$\frac{4}{5}$) | B. | ($\frac{3}{10},\frac{12}{5}$) | C. | [-$\frac{12}{5}$,-$\frac{3}{10}$] | D. | [-$\frac{3}{10}$,-$\frac{12}{5}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代号i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 年生活垃圾无害化处理量y | 0.7 | 1.1 | 1.4 | 2.2 | 2.6 | 3.0 | 3.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com