【题目】
，
是两个平面，m，n是两条直线，有下列四个命题；
①如果
，
，
，那么
.
②如果，
，那么.
③如果
，
，那么
.
④如果
，，那么m与所成的角和n与所成的角相等.
其中正确的命题的个数为（ ）
A.1B.2C.3D.4
【答案】C
【解析】
对①，运用长方体模型，找出符合条件的直线和平面，即可判断；
对②，运用线面平行的性质定理和线面垂直的性质定理，即可判断；
对③，运用面面平行的性质定理，即可判断；
对④，由平行的传递性及线面角的定义，即可判断④．
对于命题①，可运用长方体举反例证明其错误：如图，
不妨设
为直线m，
为直线n，
所在的平面为
，
所在的平面为
，显然这些直线和平面满足题目条件，但
不成立；
命题②正确，证明如下：设过直线n的某平面与平面相交于直线l，则
，由
知
，从而
，结论正确；
由平面与平面平行的定义知命题如果
，
，那么
.③正确；
由平行的传递性及线面角的定义知命题：如果
，，那么m与所成的角和n与所成的角相等，④正确.
故选：C.
科目：高中数学 来源： 题型：
【题目】自2009年以来，菜鸟网络物流和淘宝商城双十一活动已经走过十年，某数学兴趣小组收集了近五年双十一当天菜鸟网络物流订单数据如下表.并且查知这五年订单数的平均数约为6.5亿件.
年份代码 | 1 | 2 | 3 | 4 | 5 |
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
订单数 | 2.8 | 4.7 |
| 8.1 | 10.4 |
（1）现发现表中一个数据
看不清，试求出表中的值，并根据收集的这些数据和下列有关参考数据说明函数
，
中，哪一个类型更适合
关于
的回归方程；
（2）依据你的判断，求关于的回归方程；
（3）预测菜鸟网络物流2019年的订单数.
参考数据：
订单数 | 2.8 | 4.7 |
| 8.1 | 10.4 |
| 1.03 | 1.55 | 1.87 | 2.09 | 2.34 |
，
.
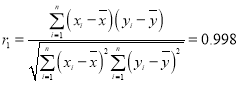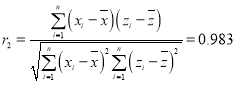参考公式：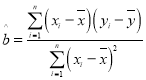
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的长轴长为
，焦距为2，抛物线
的准线经过C的左焦点F.
（1）求C与M的方程；
（2）直线l经过C的上顶点且l与M交于P，Q两点，直线FP，FQ与M分别交于点D（异于点P），E（异于点Q），证明:直线DE的斜率为定值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2018年是中国改革开放的第40周年，为了充分认识新形势下改革开放的时代性，某地的民调机构随机选取了该地的100名市民进行调查，将他们的年龄分成6段：
，并绘制了如图所示的频率分布直方图.
（1）现从年龄在
内的人员中按分层抽样的方法抽取8人，再从这8人中随机抽取3人进行座谈，用
表示年龄在
内的人数，求的分布列和数学期望；
（2）若用样本的频率代替概率，用随机抽样的方法从该地抽取20名市民进行调查，其中有
名市民的年龄在
的概率为
.当
最大时，求的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
：
过点
，过坐标原点
作两条互相垂直的射线与椭圆分别交于
，
两点.
（1）证明：当
取得最小值时，椭圆的离心率为
.
（2）若椭圆的焦距为2，是否存在定圆与直线
总相切？若存在，求定圆的方程；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某厂生产某产品的年固定成本为250万元，每生产
千件，需另投入成本
（万元），若年产量不足
千件， 
的图像是如图的抛物线，此时
的解集为
，且
的最小值是
，若年产量不小于
千件， 
，每千件商品售价为50万元，通过市场分析，该厂生产的商品能全部售完；
（1）写出年利润
（万元）关于年产量
（千件）的函数解析式；
（2）年产量为多少千件时，该厂在这一商品的生产中所获利润最大？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
