Question

已知函数f（x）=

1

3

x3+

1

2

ax2+bx+c在x1处取得极大值，在x2处取得极小值，满足x₁∈（-1，1），x₂∈（2，4），则a+2b的取值范围是

（-5，1）

．

Answer 1

分析：求函数的导数，利用函数极值关系得到x₁，x₂，是f'（x）=0的两个根，利用一元二次根的分别确定2b的取值范围即可

解答：解：∵f（x）=

1

3

x3+

1

2

ax2+bx+c在x1处取得极大值，在x2处取得极小值，
∴f'（x）=x²+ax+b，且x₁，x₂是f'（x）=0的两个根，
∵x₁∈（-1，1），x₂∈（2，4），
∴

f′(-1)＞0 f′(1)＜0 f′(2)＜0 f′(4)＞0

，即

1-a+b＞0 1+a+b＜0 4+2a+b＜0 16+4a+b＞0

，
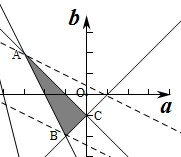
作出不等式组对应的平面区域如图（阴影部分）：
设z=a+2b，则b=-

1

2

a+

z

2

，
平移直线b=-

1

2

a+

z

2

，由图象可知当直线b=-

1

2

a+

z

2

经过点A时，直线的截距最大，此时z最大，
由

4+2a+b=0 1+a+b=0

，
解得

a=-3 b=2

，即A（-3，2），
代入z=a+2b得z的最大值为z=-3+4=1．
经过点B时，直线的截距最小，此时z最小，
由

4+2a+b=0 1-a+b=0

，
解得

a=-1 b=-2

，
即B（-1，-2），
代入z=a+2b得z的最小值为z=-1-4=-5．
即-5＜z＜1，
∴a+2b的取值范围是（-5，1）．
故答案为：（-5，1）．

点评：本题主要考查函数极值与导数之间的关系，以及一元二次根的分别，利用线性规划的知识解决a+2b的取值范围，涉及的知识点较多，综合性较强．