
分析 命题p:当x∈[0,1]时,$1≤{({\frac{1}{2}})^{x-1}}≤2$,要使${({\frac{1}{2}})^{x-1}}-m≥0$恒成立,需满足m≤$[(\frac{1}{2})^{x-1}]_{min}$.命题q:$f(x)=\sqrt{3}sinx+cosx-m=2sin({x+\frac{π}{6}})-m$,当$x∈[{-\frac{π}{6},\frac{π}{3}}]$时,$0≤x+\frac{π}{6}≤\frac{π}{2}$,$0≤2sin({x+\frac{π}{6}})≤2$,要使$?x∈[{-\frac{π}{6},\frac{π}{3}}]$,函数$f(x)=\sqrt{3}sinx+cosx-m$有零点,即可得出m的取值范围.因为命题“p∧q”为真命题,所以p真,q真,进而得出.
解答 解:命题p:当x∈[0,1]时,$1≤{({\frac{1}{2}})^{x-1}}≤2$,要使${({\frac{1}{2}})^{x-1}}-m≥0$恒成立,需满足m≤1;
命题q:$f(x)=\sqrt{3}sinx+cosx-m=2sin({x+\frac{π}{6}})-m$,当$x∈[{-\frac{π}{6},\frac{π}{3}}]$时,$0≤x+\frac{π}{6}≤\frac{π}{2}$,$0≤2sin({x+\frac{π}{6}})≤2$,要使$?x∈[{-\frac{π}{6},\frac{π}{3}}]$,函数$f(x)=\sqrt{3}sinx+cosx-m$有零点,需满足0≤m≤2,
因为命题“p∧q”为真命题,所以p真,q真,
所以0≤m≤1.
点评 本题考查了复合命题真假的判定方法、函数的单调性,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
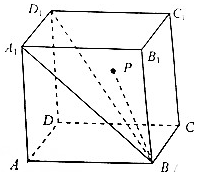 在正方体ABCD-A1B1C1D1中,点P在CDD1C1所在的平面上,满足∠PBD1=∠A1BD1,则动点P的轨迹是( )
在正方体ABCD-A1B1C1D1中,点P在CDD1C1所在的平面上,满足∠PBD1=∠A1BD1,则动点P的轨迹是( )| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,∠ABC=60°,PA=AB=BC,AD=$\frac{2\sqrt{3}}{3}$AB,E是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,∠ABC=60°,PA=AB=BC,AD=$\frac{2\sqrt{3}}{3}$AB,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-y+1=0 | B. | 2x-y-4=0 | C. | x+2y-2=0 | D. | x+2y-4=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com