练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】中国古代几何中的勾股容圆，是阐述直角三角形中内切圆问题． 此类问题最早见于《九章算术》“勾股”章，该章第16题为：“今有勾八步，股十五步． 问勾中容圆，径几何？”意思是“直角三角形的两条直角边分别为8和15，则其内切圆直径是多少？”若向上述直角三角形内随机抛掷120颗米粒（大小忽略不计，取），落在三角形内切圆内的米粒数大约为（ ）

    A.54B.48C.42D.36

    【答案】A

    【解析】

    求出直角三角形斜边长，代入直角三角形内切圆半径公式求得内切圆半径，再求出三角形面积及内切圆面积，利用几何概型中面积型概率公式求解即可.

    直角三角形的斜边长为，所以该三角形内切圆半径为，

    所以向该直角三角形内随机抛掷120颗米粒，落在圆内的数量为颗.

    故选A

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设是各项均为正数的等差数列，，是和的等比中项，的前项和为，.

    （1）求和的通项公式;

    （2）设数列的通项公式.

    （i）求数列的前项和；

    （ii）求.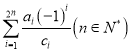

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】环境问题是当今世界共同关注的问题，且多种多样，中国环境十大问题是指大气污染问题、水环境污染问题、垃圾处理问题、土地荒漠化和沙灾问题、水土流失问题、旱灾和水灾问题、生物多样性破坏问题、WTO与环境问题、三峡库区的环境问题、持久性有机物污染问题.其中大气环境面临的形势非常严峻，大气污染物排放总量居高不下，我国环保总局根据空气污染指数PM2.5浓度，制定了空气质量标准（前者是空气污染指数，后者是空气质量等级）：（1）优；（2）良；（3）轻度污染；（4）中度污染；（5）重度污染；（6）严重污染.辽宁省某市政府为了改善空气质量，节能减排，从2012年开始考察了连续六年12月份的空气污染指数，绘制了频率分布直方图如图，经过分析研究，决定从2018年12月1日起在空气质量重度污染和严重污染的日子对机动车辆施行限号出行，请根据这段材料回答以下两个问题：

    ①若按分层抽样的方法，从空气质量等级为优与良的天气中抽取5天，再从这5天中随机抽取2天，求至少有一天空气质量是优的概率；

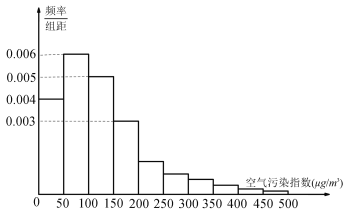
    ②该市环保局为了调查汽车尾气排放对空气质量的影响，对限行两年来的12月份共60天的空气质量进行统计，其结果如下表：

    空气质量

    优

    良

    轻度污染

    中度污染

    重度污染

    严重污染

    天数

    12

    28

    11

    6

    2

    1

    根据限行前6年180天与限行后60天的数据，计算并填写列联表，并回答是否有95%的把握认为空气质量的优良与汽车尾气的排放有关.

    空气质量优、良

    空气质量污染

    总计

    限行前

    限行后

    总计

    参考数据：

    0.10

    0.05

    0.025

    0.010

    0.005

    2.706

    3.841

    5.024

    6.635

    7.879

    参考公式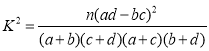，其中.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线的参数方程为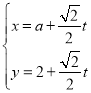（为参数），以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为．

    （1）求直线和曲线的直角坐标方程；

    （2）若点坐标为，直线与曲线交于两点，且，求实数的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设无穷数列的每一项均为正数，对于给定的正整数，()，若是等比数列，则称为数列.

    （1）求证：若是无穷等比数列，则是数列；

    （2）请你写出一个不是等比数列的数列的通项公式；

    （3）设为数列，且满足，请用数学归纳法证明：是等比数列.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】关于的方程有3个不等实根．

    （1）求实数的取值范围；

    （2）求证：方程的3个实根之和大于2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知平面四边形ABCD是菱形，，，将沿对角线BD翻折至的位置，且二面角的平面角为，则三棱锥的外接球的表面积为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】成都七中为了解班级卫生教育系列活动的成效，对全校40个班级进行了一次突击班级卫生量化打分检查（满分100分，最低分20分）.根据检查结果：得分在评定为“优”，奖励3面小红旗；得分在评定为“良”，奖励2面小红旗；得分在评定为“中”，奖励1面小红旗；得分在评定为“差”，不奖励小红旗.已知统计结果的部分频率分布直方图如图：

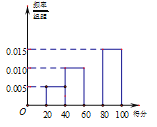
    （1）依据统计结果的部分频率分布直方图，求班级卫生量化打分检查得分的中位数；

    （2）学校用分层抽样的方法，从评定等级为“良”、“中”的班级中抽取6个班级，再从这6个班级中随机抽取2个班级进行抽样复核，求所抽取的2个班级获得的奖励小红旗面数和不少于3的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】方舱医院的启用在本次武汉抗击新冠疫情的关键时刻起到了至关重要的作用，图1为某方舱医院的平面设计图，其结构可以看成矩形在四个角处对称地截去四个全等的三角形所得，图2中所示多边形，整体设计方案要求：内部井字形的两根水平横轴米，两根竖轴米，记整个方舱医院的外围隔离线（图2实线部分，轴和边框的粗细忽略不计）总长度为，与、的交点为、，与、的交点为、，（）.

    （1）若，且两根横轴之间的距离米，求外围隔离线总长度；

    （2）由于疫情需要，外围隔离线总长度不超过240米，当整个方舱医院（多边形的面积）最大时，给出此设计方案中的大小与的长度.

    查看答案和解析>>

    同步练习册答案