练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆（）的左右焦点分别为、，离心率.过的直线交椭圆于、两点，三角形的周长为.

    （1）求椭圆的方程；

    （2）若弦，求直线的方程.

    【答案】（1）;（2）.

    【解析】试题分析：（1）利用椭圆的离心率以及的周长为8，求出a，c，b，即可得到椭圆的方程，
    （2）求出直线方程与椭圆方程联立，点的坐标为, 的坐标为求出A，B坐标，然后求解三角形的面积即可．

    试题解析：

    （1）三角形的周长，所以.

    离心率，所以，则.

    椭圆的方程为：

    （2）设点的坐标为, 的坐标为， 的斜率为（显然存在）

    .

    .

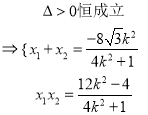
    点睛: 本题主要考查直线与圆锥曲线位置关系，所使用方法为韦达定理法：因直线的方程是一次的，圆锥曲线的方程是二次的，故直线与圆锥曲线的问题常转化为方程组关系问题，最终转化为一元二次方程问题，故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一，尤其是弦中点问题，弦长问题，可用韦达定理直接解决，但应注意不要忽视判别式的作用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】下列说法正确的是（ ）

    A. 一枚骰子掷一次得到2点的概率为，这说明一枚骰子掷6次会出现一次2点

    B. 某地气象台预报说，明天本地降水的概率为70%，这说明明天本地有70%的区域下雨，30%的区域不下雨

    C. 某中学高二年级有12个班，要从中选2个班参加活动，由于某种原因，一班必须参加，另外再从二至十二班中选一个班，有人提议用如下方法：掷两枚骰子得到的点数是几，就选几班，这是很公平的方法

    D. 在一场乒乓球赛前，裁判一般用掷硬币猜正反面来决定谁先打球，这应该说是公平的

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】己知函数f（x）=（x+l）lnx﹣ax+a （a为正实数，且为常数）
    （1）若f（x）在（0，+∞）上单调递增，求a的取值范围；
    （2）若不等式（x﹣1）f（x）≥0恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】全网传播的融合指数是衡量电视媒体在中国网民中影响力的综合指标，根据相关报道提供的全网传播2017年某全国性大型活动的“省级卫视新闻台”融合指数的数据，对名列前20名的“省级卫视新闻台”的融合指数进行分组统计，结果如表所示.

    组号

    分组

    频数

    1

    2

    2

    8

    3

    7

    4

    3

    （1）根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数;

    （2）现从融合指数在和内的“省级卫视新闻台”中随机抽取2家进行调研，求至少有1家的融合指数在内的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

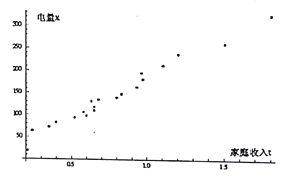
    【题目】为了实现绿色发展，避免浪费能源，耨市政府计划对居民用电采用阶梯收费的方法.为此，相关部门在该市随机调查了20户居民六月份的用电量（单位：）和家庭收入（单位：万元），以了解这个城市家庭用电量的情况．

    用电量数据如下：18,63,72,82,93,98,106,110,118,130,134,139,147,163,180,194,212,237,260,324．

    对应的家庭收入数据如下：0.21，0.24，0.35,0.40,0.52,0.60,0.58,0.65,0.65,0.63,0.68,0.80,0.83，0.93,0.97,0.96,1.1,1.2,1.5,1.8.

    （1）根据国家发改委的指示精神，该市计划实施3阶阶梯电价，使75%的用户在第一档，电价为0.56元/；的用户在第二档，电价为0.61元/；的用户在第三档，电价为0.86元/；试求出居民用电费用与用电量间的函数关系式；

    （2）以家庭收入为横坐标，电量为纵坐标作出散点图（如图），求关于的回归直线方程（回归直线方程的系数四舍五入保留整数）；

    （3）小明家的月收入7000元，按上述关系，估计小明家月支出电费多少元？

    参考数据：，，，，．

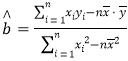    参考公式：一组相关数据的回归直线方程的斜率和截距的最小二乘法估计分别为．，，其中为样本均值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，已知中心在原点，离心率为的椭圆的一个焦点为圆： 的圆心．

    （Ⅰ）求椭圆的方程；

    （Ⅱ）设是椭圆上一点，过作两条斜率之积为的直线， ，当直线， 都与圆相切时，求的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

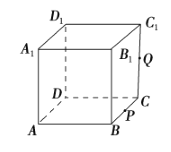
    【题目】如图，正方体的棱长为 1， 为的中点， 为线段上的动点，过点A、P、Q的平面截该正方体所得的截面记为.则下列命题正确的是__________(写出所有正确命题的编号)．

    ①当时， 为四边形；②当时， 为等腰梯形；③当时， 为六边形；④当时， 的面积为.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，三棱柱中，底面为正三角形， 底面，且， 是的中点.

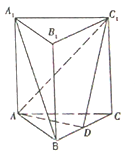
    （1）求证： 平面；

    （2）求证：平面平面；

    （3）在侧棱上是否存在一点，使得三棱锥的体积是？若存在，求出的长；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点M是圆心为E的圆上的动点，点，线段MF的垂直平分线交EM于点P.

    （Ⅰ）求动点P的轨迹C的方程；

    （Ⅱ）过原点O作直线交（Ⅰ）中轨迹C于点A、B，点D满足，试求四边形AFBD的面积的取值范围.

    查看答案和解析>>

    同步练习册答案