
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
科目:高中数学 来源: 题型:填空题
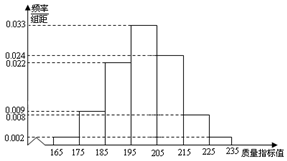 从某企业的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:求这500件产品质量指标值的样本平均数$\overline{x}$和样本方差s2(同一组数据用该区间的中点值作代表).
从某企业的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:求这500件产品质量指标值的样本平均数$\overline{x}$和样本方差s2(同一组数据用该区间的中点值作代表).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{6}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 28π | B. | $\frac{{28\sqrt{7}π}}{3}$ | C. | 32π | D. | $\frac{{64\sqrt{2}π}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{4}$个单位,再向上平移1个单位 | |
| B. | 向左平移$\frac{π}{4}$个单位,再向下平移1个单位 | |
| C. | 向右平移$\frac{π}{2}$个单位,再向上平移1个单位 | |
| D. | 向左平移$\frac{π}{2}$个单位,再向下平移1个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{5}}}{5}$ | B. | $\frac{{3\sqrt{3}}}{4}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
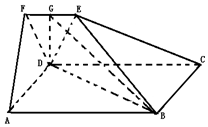 如图,在五面体ABCDEF中,四边形ABCD为正方形,EF∥CD,平面CDFE⊥平面ABCD,且AD=3EF,DE=DF,点G为EF中点.
如图,在五面体ABCDEF中,四边形ABCD为正方形,EF∥CD,平面CDFE⊥平面ABCD,且AD=3EF,DE=DF,点G为EF中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com