
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,且C与y轴交于
,且C与y轴交于![]() 两点.
两点.
(1)求椭圆C的标准方程;
(2)设P点是椭圆C上的一个动点且在y轴的右侧,直线PA,PB与直线![]() 交于M,N两点.若以MN为直径的圆与x轴交于E,F两点,求P点横坐标的取值范围.
交于M,N两点.若以MN为直径的圆与x轴交于E,F两点,求P点横坐标的取值范围.
【答案】(1) ![]() ;(2)见解析.
;(2)见解析.
【解析】
试题分析:(1)由椭圆![]() 的焦距为
的焦距为![]() ,可得
,可得![]() ,由
,由![]() 可得
可得![]() ,结合
,结合![]() 可得
可得![]() ,进而可得结果;(2)设
,进而可得结果;(2)设![]() ,可得
,可得![]() ,直线
,直线![]() 的方程为
的方程为![]() ,同理得直线
,同理得直线![]() 的方程为
的方程为![]() , 求得
, 求得![]() ,
,![]() ,可得圆的方程为
,可得圆的方程为![]() ,利用这个圆与
,利用这个圆与![]() 轴相交,方程有两个不同的实数解,即可得结果.
轴相交,方程有两个不同的实数解,即可得结果.
试题解析:(Ⅰ)由题意可得,![]() ,
,![]() 所以
所以![]() ,, 椭圆
,, 椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)设![]() ,
,![]() ,
,![]() ,
,
所以![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
同理得直线![]() 的方程为
的方程为![]() ,
,
直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,
,
直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,线段
,线段![]() 的中点
的中点![]() ,
,
所以圆的方程为![]() .
.
令![]() ,则
,则![]() , 因为
, 因为![]() ,所以
,所以![]() ,
,
因为这个圆与![]() 轴相交,所以该方程有两个不同的实数解,
轴相交,所以该方程有两个不同的实数解,
则![]() ,又0
,又0![]() ,解得
,解得![]() .
.
解法二:直线![]() 的方程为
的方程为![]() ,与椭圆
,与椭圆![]() 联立得:
联立得:![]() ,
,![]() ,
,
同理设![]() 直线的方程为
直线的方程为![]() 可得
可得![]() ,
,
由![]()
![]() ,可得
,可得![]() ,
,
所以![]() ,
,![]() ,
,![]() 的中点为
的中点为![]() ,
,
所以![]() 为直径的圆为
为直径的圆为![]() .
.
![]() 时,
时,![]() ,所以
,所以![]() ,
,
因为![]() 为直径的圆与
为直径的圆与![]() 轴交于
轴交于![]() 两点,所以
两点,所以![]() ,
,
代入![]() 得:
得:![]() ,所以
,所以![]() ,
,
所以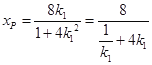 在
在![]() 单增,在
单增,在![]() 单减,所以
单减,所以![]() .
.


科目:高中数学 来源: 题型:
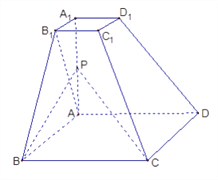
【题目】已知四棱台![]() 的上下底面分别是边长为2和4的正方形,
的上下底面分别是边长为2和4的正方形, ![]() = 4且
= 4且 ![]() ⊥底面
⊥底面![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
(Ⅰ)求证: ![]() 面
面 ![]() ;
;
(Ⅱ)在![]() 边上找一点
边上找一点![]() ,使
,使![]() ∥面
∥面![]() ,
,
并求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象为不间断的曲线,定义域为
的图象为不间断的曲线,定义域为![]() ,规定:
,规定:
①如果对于任意![]() ,
,![]() 都有
都有![]() ,则称函数
,则称函数![]() 是凹函数.
是凹函数.
②如果对于任意![]() ,
,![]() 都有
都有![]() ,则称函数
,则称函数![]() 是凸函数.
是凸函数.
(1)若函数![]() (
(![]() 且
且![]() )是凹函数,试写出实数
)是凹函数,试写出实数![]() 的取值范围;(直接写出结果,无需证明);
的取值范围;(直接写出结果,无需证明);
(2)判断函数![]() 是凹函数还是凸函数,并加以证明;
是凹函数还是凸函数,并加以证明;
(3)若对任意的![]() 且
且![]() ,
,![]() ,试证明存在
,试证明存在![]() ,使
,使![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(x+2),g(x)=loga(2﹣x)(a>0,a≠1).
(1)求函数f(x)﹣g(x)的定义域;
(2)判断f(x)﹣g(x)的奇偶性并证明;
(3)求f(x)﹣g(x)>0中x取值范围,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:2x﹣y+2=0与l2:x+y+4=0.
(1)若一条光线从l1与l2的交点射出,与x轴交于点P(3,0),且经x轴反射,求反射光线所在直线的方程;
(2)若直线l经过点P(3,0),且它夹在直线l1与l2之间的线段恰被点P平分,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】常州地铁项目正在紧张建设中,通车后将给市民出行带来便利.已知某条线路通车后,地铁的发车时间间隔 ![]() (单位:分钟)满足
(单位:分钟)满足![]() ,
,![]() .经测算,地铁载客量与发车时间间隔
.经测算,地铁载客量与发车时间间隔![]() 相关,当
相关,当![]() 时地铁为满载状态,载客量为1200人,当
时地铁为满载状态,载客量为1200人,当![]() 时,载客量会减少,减少的人数与
时,载客量会减少,减少的人数与![]() 的平方成正比,且发车时间间隔为2分钟时的载客量为560人,记地铁载客量为
的平方成正比,且发车时间间隔为2分钟时的载客量为560人,记地铁载客量为![]() .
.
⑴ 求![]() 的表达式,并求当发车时间间隔为6分钟时,地铁的载客量;
的表达式,并求当发车时间间隔为6分钟时,地铁的载客量;
⑵ 若该线路每分钟的净收益为![]() (元),问当发车时间间隔为多少时,该线路每分钟的净收益最大?
(元),问当发车时间间隔为多少时,该线路每分钟的净收益最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知圆
中,已知圆![]() :
:![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,圆
轴的正半轴为极轴,取相同的长度单位建立极坐标系,圆![]() 的极坐标方程
的极坐标方程![]() .
.
(1)分别写出圆![]() 的普通方程与圆
的普通方程与圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与圆
与圆![]() 的公共弦的端点为
的公共弦的端点为![]() ,圆
,圆![]() 的圆心为
的圆心为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com