
【题目】已知函数![]() ,
,![]() ,其中a为常数.
,其中a为常数.
![]() 当
当![]() 时,设函数
时,设函数![]() ,判断函数
,判断函数![]() 在
在![]() 上是增函数还是减函数,并说明理由;
上是增函数还是减函数,并说明理由;
![]() 设函数
设函数![]() ,若函数
,若函数![]() 有且仅有一个零点,求实数a的取值范围.
有且仅有一个零点,求实数a的取值范围.
【答案】(1)见解析;(2)![]() ,
,![]()
【解析】
![]() 代入a的值,求出
代入a的值,求出![]() 的解析式,判断函数的单调性即可;
的解析式,判断函数的单调性即可;
![]() 由题意把函数
由题意把函数![]() 有且仅有一个零点转化为
有且仅有一个零点转化为![]() 有且只有1个实数根,通过讨论a的范围,结合二次函数的性质得到关于a的不等式组,解出即可.
有且只有1个实数根,通过讨论a的范围,结合二次函数的性质得到关于a的不等式组,解出即可.
(1)由题意,当![]() 时,
时,![]() ,则
,则![]() ,
,
因为![]() ,又由
,又由![]() 在
在![]() 递减,
递减,
所以![]() 在
在![]() 递增,
递增,
所以根据复合函数的单调性,可得函数![]() 在
在![]() 单调递增函数;
单调递增函数;
![]() 由
由![]() ,得
,得![]() ,即
,即![]() ,
,
若函数![]() 有且只有1个零点,
有且只有1个零点,
则方程![]() 有且只有1个实数根,
有且只有1个实数根,
化简得![]() ,
,
即![]() 有且只有1个实数根,
有且只有1个实数根,
![]() 时,
时,![]() 可化为
可化为![]() ,即
,即![]() ,
,
此时![]() ,满足题意,
,满足题意,
![]() 当
当![]() 时,由
时,由![]() 得:
得:
![]() ,解得:
,解得:![]() 或
或![]() ,
,
![]() 当
当![]() 即
即![]() 时,方程
时,方程![]() 有且只有1个实数根,
有且只有1个实数根,
此时![]() ,满足题意,
,满足题意,
![]() 当
当![]() 即
即![]() 时,
时,
若![]() 是
是![]() 的零点,则
的零点,则![]() ,解得:
,解得:![]() ,
,
若![]() 是
是![]() 的零点,则
的零点,则 ,解得:
,解得:![]() ,
,
![]() 函数
函数![]() 有且只有1个零点,所以
有且只有1个零点,所以![]() 或
或![]() ,
,![]() ,
,
综上,a的范围是![]() ,
,![]() .
.


科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知抛物线C的方程C:y2="2" p x(p>0)过点A(1,-2).
(I)求抛物线C的方程,并求其准线方程;
(II)是否存在平行于OA(O为坐标原点)的直线l,使得直线l与抛物线C有公共点,且直线OA与l的距离等于![]() ?若存在,求出直线l的方程;若不存在,说明理由。
?若存在,求出直线l的方程;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AA1=AC,且AB⊥AC,D,E分别为是A1C1和BB1的中点.
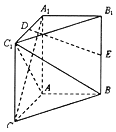
(1)求证:A1C⊥平面ABC1;
(2)求证:DE![]() 平面ABC1
平面ABC1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com