
【题目】设函数![]() ,g(x)=x2+bx,若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是( )
,g(x)=x2+bx,若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率
,离心率![]() ,且椭圆的短轴长为2.
,且椭圆的短轴长为2.
(1)球椭圆的标准方程;
(2)已知直线![]() 过右焦点
过右焦点![]() ,且它们的斜率乘积为
,且它们的斜率乘积为![]() ,设
,设![]() 分别与椭圆交于点
分别与椭圆交于点![]() 和
和![]() .
.
①求![]() 的值;
的值;
②设![]() 的中点
的中点![]() ,
,![]() 的中点为,求
的中点为,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的发展,居民的储蓄存款逐年增长。设某地区城乡居民人民币储蓄存款![]() (单位:亿元)的数据如下:
(单位:亿元)的数据如下:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
储蓄存款 | 3.4 | 3.6 | 4.5 | 4.9 | 5.5 | 6.1 | 7.0 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)2018年城乡居民储蓄存款前五名中,有三男和两女。现从这5人中随机选出2人参加某访谈节目,求选中的2人性别不同的概率。
附:回归直线的斜率和截距的最小二乘估计公式分别为: ,
,![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
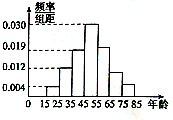
【题目】某购物中心为了了解顾客使用新推出的某购物卡的顾客的年龄分布情况,随机调查了![]() 位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间
位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间![]() 内的频率之比为
内的频率之比为![]() .
.
(1) 求顾客年龄值落在区间![]() 内的频率;
内的频率;
(2) 拟利用分层抽样从年龄在![]() 的顾客中选取
的顾客中选取![]() 人召开一个座谈会,现从这
人召开一个座谈会,现从这![]() 人中选出
人中选出![]() 人,求这两人在不同年龄组的概率.
人,求这两人在不同年龄组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有2000名职工,老年、中年、青年分布在管理、技术开发、营销、生产各部门中,如下表所示:
人数 | 管理 | 技术开发 | 营销 | 生产 | 共计 |
老年 | 40 | 40 | 40 | 80 | 200 |
中年 | 80 | 120 | 160 | 240 | 600 |
青年 | 40 | 160 | 280 | 720 | 1 200 |
小计 | 160 | 320 | 480 | 1 040 | 2 000 |
(1)若要抽取40人调查身体状况,则应怎样抽样?
(2)若要开一个25人的讨论单位发展与薪金调整方面的座谈会,则应怎样抽选出席人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,圆
,圆![]() 经过椭圆
经过椭圆![]() 的两个焦点和两个顶点,点
的两个焦点和两个顶点,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() ,
,![]() .
.
(Ⅰ)求椭圆![]() 的方程和点
的方程和点![]() 的坐标;
的坐标;
(Ⅱ)过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,过点
两点,过点![]() 与
与![]() 垂直的直线
垂直的直线![]() 与椭圆
与椭圆![]() 相交于另一点
相交于另一点![]() ,求
,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某城市拟在矩形区域![]() 内修建儿童乐园,已知
内修建儿童乐园,已知![]() 百米,
百米,![]() 百米,点E,N分别在AD,BC上,梯形
百米,点E,N分别在AD,BC上,梯形![]() 为水上乐园;将梯形EABN分成三个活动区域,
为水上乐园;将梯形EABN分成三个活动区域,![]() 在
在![]() 上,且点B,E关于MN对称.现需要修建两道栅栏ME,MN将三个活动区域隔开.设
上,且点B,E关于MN对称.现需要修建两道栅栏ME,MN将三个活动区域隔开.设![]() ,两道栅栏的总长度
,两道栅栏的总长度![]() .
.

(1)求![]() 的函数表达式,并求出函数的定义域;
的函数表达式,并求出函数的定义域;
(2)求![]() 的最小值及此时
的最小值及此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() :
:![]() ,椭圆
,椭圆![]() :
:![]() ,
,![]() 为椭圆右顶点.过原点
为椭圆右顶点.过原点![]() 且异于坐标轴的直线与椭圆
且异于坐标轴的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() 与
与![]() 的另一交点为
的另一交点为![]() ,直线
,直线![]() 与
与![]() 的另一交点为
的另一交点为![]() ,其中
,其中![]() .设直线
.设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .
.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)记直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,是否存在常数
,是否存在常数![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 值;若不存在,说明理由.
值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com