Question

3．如图，定义在[-1，2]上的函数f（x）的图象为折线段ACB，
（1）求函数f（x）的解析式；
（2）请用数形结合的方法求不等式f（x）≥log₂（x+1）的解集，不需要证明．

Answer 1

分析 （1）利用待定系数法求函数f（x）的解析式；
（Ⅱ）根据函数的图象确定函数值对应的取值范围．

解答 解：（1）根据图象可知点A（-1，0），B（0，2），C（2，0），所以$f（x）=\left\{{\begin{array}{l}{2x+2，（-1≤x≤0）}\\{-x+2，（0＜x≤2）}\end{array}}\right.$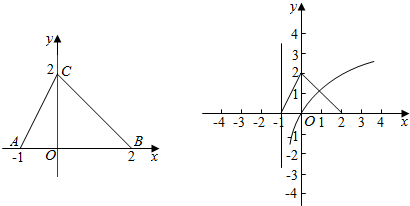

（2）根据（1）可得函数f（x）的图象经过点（1，1），而函数log₂（x+1）也过点（1，1），
函数log₂（x+1）的图象可以由log₂x左移1个单位而来，
如图所示，所以根据图象可得不等式f（x）≥log₂（x+1）的解集是（-1，1]．

点评 本题主要考查函数解析式的求法，利用待定系数法是解决本题的关键．