由已知得,
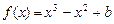
,又
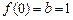
,所以
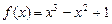
.
由
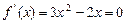
,得
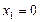
,
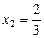
.
根据
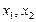
列表,分析
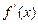
的符号和函数的单调性.
由上表,得函数
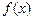
的极小值为
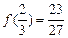
,极大值为
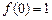
,又
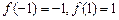
,所以函数
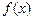
在区间
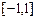
上的最小值为
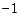
,最大值为1.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(12分)已知函数f(x)=
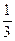
ax
3-bx
2 +(2-b)x+1,在x=x
2处取得极大值,在x=x
2处取得极小值,且0<x
1<1<x
2<2。
(1)证明:a>0;
(2)若z=a+2b,求z的取值范围。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
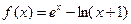
。
(I)求函数
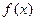
的最小值; (Ⅱ)已知
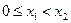
,求证:
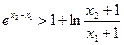
。
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知函数
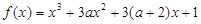
无极值,且对任意的
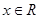
都有不等式
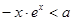
恒成立,则满足条件的实数
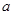
的取值范围是
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
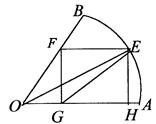
如图,扇形
AOB的半径为1,中心角为45°,矩形E
FGH内接于扇形,求矩形对角线长的最小值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知函数
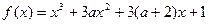
有极大值又有极小值,则
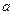
的取值范围是
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
函数
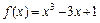
在区间[
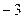
,0]上的最小值是
查看答案和解析>>

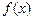 的导数
的导数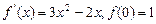 .求函数
.求函数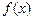 在区间
在区间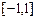 上的最小值与最大值.
上的最小值与最大值. 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案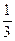 ax3-bx2 +(2-b)x+1,在x=x2处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2。
ax3-bx2 +(2-b)x+1,在x=x2处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2。