Question

1．已知抛物线C₁：y²=2px（p＞0）与椭圆C₂：x²+2y²=m²（m＞0）的一个交点为P（1，t），点F是抛物线C₁的焦点．且|PF|=$\frac{3}{2}$．
（Ⅰ）求p，t，m的值；
（Ⅱ）设O为坐标原点，椭圆C₂上是否存在点A（不考虑点A为C₂的顶点），使得过点O作线段OA的垂线与抛物线C₁交于点B，直线AB交y轴于点E，满足∠0AE=∠E0B？若存在，求点A的坐标；若不存在，说明理由．

Answer 1

分析 （Ⅰ）利用抛物线的定义求p，点的坐标代入求出t，m的值；
（Ⅱ）设出OA，OB的方程于椭圆、抛物线分别联立，求出A的横坐标，利用∠0AE=∠E0B，分类讨论，即可得出结论．

解答 解：（Ⅰ）由题意1+$\frac{p}{2}$=$\frac{3}{2}$，∴p=1，∴抛物线C₁：y²=2x，
（1，t）代入y²=2x，∴t=±$\sqrt{2}$，
（1，$±\sqrt{2}$）代入椭圆C₂：x²+2y²=m²（m＞0），∴m=$\sqrt{5}$；
（Ⅱ）设OA的斜率为k，则OB的斜率为-$\frac{1}{k}$，
由$\left\{\begin{array}{l}{y=kx}\\{{x}^{2}+2{y}^{2}=5}\end{array}\right.$，可得x=±$\sqrt{\frac{5}{1+2{k}^{2}}}$；
由$\left\{\begin{array}{l}{y=-\frac{1}{k}x}\\{{y}^{2}=2x}\end{array}\right.$，可得x=2k²，
若∠0AE=∠E0B，则根据对称性，考虑A在第一、三象限的情形．
A在第一象限，则A（$\sqrt{\frac{5}{1+2{k}^{2}}}$，k$\sqrt{\frac{5}{1+2{k}^{2}}}$），B（2k²，-2k），且$\sqrt{\frac{5}{1+2{k}^{2}}}$≠2k²，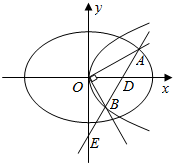

设直线AB与x轴相交于D，
∵∠0AE=∠E0B，∠DOE=∠A0B=90°，
∴∠0AD=∠A0D，∠0BD=∠D0B，
∴AD=OD=BD，
∴D是AB的中点，
∴k$\sqrt{\frac{5}{1+2{k}^{2}}}$=2k，∴k²=$\frac{1}{8}$，∴A（2，$\frac{\sqrt{2}}{2}$）；
A在第二象限，k＜0则A（-$\sqrt{\frac{5}{1+2{k}^{2}}}$，-k$\sqrt{\frac{5}{1+2{k}^{2}}}$），B（2k²，-2k），且$\sqrt{\frac{5}{1+2{k}^{2}}}$≠2k²，

设直线AB与x轴相交于D，
∵∠0AE=∠E0B，∠A0B=90°，
∴∠0AE+∠A0E=∠E0B+∠A0E，
∴OE⊥AB，
∴-k$\sqrt{\frac{5}{1+2{k}^{2}}}$=-2k，∴k²=$\frac{1}{8}$，∴A（-2，$\frac{\sqrt{2}}{2}$）；
综上，A（±2，$\frac{\sqrt{2}}{2}$）或A（±2，-$\frac{\sqrt{2}}{2}$）．

点评 本题考查抛物线、椭圆的方程，考查直线与抛物线、椭圆的位置关系，考查分类讨论的数学思想，属于中档题．