
在边长为60cm的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?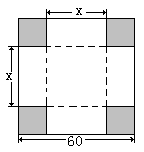
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
(本题满分10分)已知函数 ,(
,(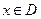 ),若同时满足以下条件:
),若同时满足以下条件:
① 在D上单调递减或单调递增
在D上单调递减或单调递增
② 存在区间[ ]
]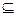 D,使
D,使 在[
在[ ]上的值域是[
]上的值域是[ ],那么称
],那么称 (
(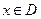 )为闭函数。
)为闭函数。
(1)求闭函数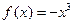 符合条件②的区间[
符合条件②的区间[ ];
];
(2)判断函数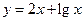 是不是闭函数?若是请找出区间[
是不是闭函数?若是请找出区间[ ];若不是请说明理由;
];若不是请说明理由;
(3)若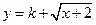 是闭函数,求实数
是闭函数,求实数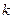 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
15分)经市场调查,某超市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间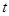 (天)的函数,且销售量近似满足函数
(天)的函数,且销售量近似满足函数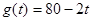 (件),价格近似满足函数
(件),价格近似满足函数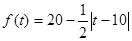 (元)。
(元)。
(1)试写出该种商品的日销售额 函数表达式;
函数表达式;
(2)求该种商品的日销售额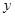 的最大值与最小值。
的最大值与最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
医学上为了研究传染病在传播的过程中病毒细胞的生长规律及其预防措施,将 个病毒细胞注入到一只小白鼠的体内进行试验.在试验过程中,得到病毒细胞的数量与时间的关系记录如下表:
个病毒细胞注入到一只小白鼠的体内进行试验.在试验过程中,得到病毒细胞的数量与时间的关系记录如下表:
| 时间(小时) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 病毒细胞总数(个) |  | 2 | 4 | 8 | 16 | 32 | 64 |

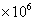 个时,小白鼠将死亡,但有一种药物对杀死此种病毒有一定效果,用药后,即可杀死其体内的大部分病毒细胞.
个时,小白鼠将死亡,但有一种药物对杀死此种病毒有一定效果,用药后,即可杀死其体内的大部分病毒细胞.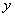 与时间
与时间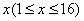 的函数关系式;
的函数关系式; )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com