
【题目】如图,已知多面体ABC﹣A1B1C1中,AA1,BB1,CC1均垂直于平面ABC,AB⊥AC,AA1=4,CC1=1,AB=AC=BB1=2.
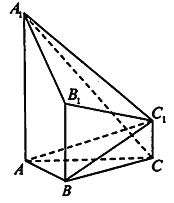
(Ⅰ)求证:A1C⊥平面ABC1;
(Ⅱ)求二面角B﹣A1B1﹣C1的余弦值.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与直线
的普通方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切.
相切. ![]() 、
、![]() 是椭圆
是椭圆![]() 的右顶点与上顶点,直线
的右顶点与上顶点,直线![]() 与椭圆相交于
与椭圆相交于![]() 、
、![]() 两点.
两点.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当四边形![]() 面积取最大值时,求
面积取最大值时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行调查,通过抽样,获得某年100为居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)求直方图的![]() 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月用水量的中位数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com