Question

【题目】设min{m，n}表示m、n二者中较小的一个，已知函数f（x）=x2+8x+14，g（x）=min{（ ）x﹣2 ， log2（4x）}（x＞0），若x1∈[﹣5，a]（a≥﹣4），x2∈（0，+∞），使得f（x1）=g（x2）成立，则a的最大值为（ ）
A.﹣4
B.﹣3
C.﹣2
D.0

Answer 1

【答案】C
【解析】解：当（ ）x﹣2=log2（4x），解得x=1， 当0＜x≤1时，（ ）x﹣2≥log2（4x），
当x＞1时，（ ）x﹣2＜log2（4x），
∴g（x）=min{（ ）x﹣2 ， log2（4x）}（x＞0）= ，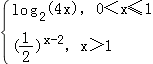
∴当0＜x≤1时，g（x）的值域为（﹣∞，2]，当x＞1时，g（x）值域为（0，2），
∴g（x）的值域为（﹣∞，2]
∵f（x）=x2+8x+14=（x+4）2﹣2，其对称轴为x=﹣4，
∴f（x）在[﹣5，﹣4]上为减函数，在（﹣4，a]上为增函数，
∵f（﹣5）=﹣1，f（a）=a2+8a+14
当﹣4≤a≤﹣3时，函数f（x）的值域为[﹣2，﹣1]，
当a＞﹣3时，函数f（x）的值域为[﹣2，a2+8a+14]，
∵x1∈[﹣5，a]（a≥﹣4），x2∈（0，+∞），使得f（x1）=g（x2）成立，
∴a2+8a+14≤2，
解得﹣3＜a≤﹣2，
综上所述a的范围为[﹣4，﹣2]，
∴a的最大值为﹣2，
故选：C
【考点精析】本题主要考查了函数的最值及其几何意义的相关知识点，需要掌握利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值才能正确解答此题．