
【题目】△ABC是等边三角形,边长为4,BC边的中点为D,椭圆W以A,D为左、右两焦点,且经过B、C两点.
(1)求该椭圆的标准方程;
(2)过点D且x轴不垂直的直线l交椭圆于M,N两点,求证:直线BM与CN的交点在一条定直线上.
【答案】
(1)解:由题意可知两焦点为 ![]() 与
与 ![]() ,可得c=
,可得c= ![]() ,2a=6,可得a=3,则b=
,2a=6,可得a=3,则b= ![]() ,
,
因此椭圆的方程为 ![]() .
.
(2)证明:①当MN不与x轴重合时,
设MN的方程为 ![]() ,且
,且 ![]() ,
, ![]() ,
,
设M(x1,y1),N(x2,y2)
联立椭圆与直线方程,可得 ![]() ,
,
消去x可得 ![]() ,
,
即 ![]() ,
, ![]()
则BM: ![]() ①CN:
①CN: ![]() ②
②
②﹣①得 ![]() ,
,
![]() ,
,
![]() ,
,
 ,
,
![]() .
.
则 ![]() ,即
,即 ![]() .
.
②当MN与x轴重合时,即MN的方程x=0为,即M(3,0),N(﹣3,0).
即BM: ![]() ①,
①,
CN: ![]() ②
②
联立①和②消去y可得 ![]() .
.
综上BM与CN的交点在直线 ![]() 上.
上.
【解析】(1)根据题意,结合椭圆的定义得出a,b,c的值,从而得到椭圆的方程,(2)对直线MN的斜率是否为零进行分别讨论,①当斜率不为零时,设出直线MN的方程为x = m y + ![]() ,且 B (
,且 B ( ![]() , 2 ) , C (
, 2 ) , C ( ![]() , 2 ) ,设M(x1,y1),N(x2,y2),联立直线方程和椭圆方程,用韦达定理表示出y1+y2, y 1 y 2,根据点的坐标表示出直线BM,直线CN的方程,联立解出x=3
, 2 ) ,设M(x1,y1),N(x2,y2),联立直线方程和椭圆方程,用韦达定理表示出y1+y2, y 1 y 2,根据点的坐标表示出直线BM,直线CN的方程,联立解出x=3![]() ,②当斜率为零时,MN的直线方程为x=0,代入计算也可得x=3
,②当斜率为零时,MN的直线方程为x=0,代入计算也可得x=3![]() ,综上结论得证.
,综上结论得证.
【考点精析】认真审题,首先需要了解椭圆的标准方程(椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() ).
).


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,0<φ<π),其导函数f′(x)的部分图象如图所示,则函数f(x)的解析式为( )
A.f(x)=4sin( ![]() x+
x+ ![]() π)
π)
B.f(x)=4sin( ![]() x+
x+ ![]() )
)
C.f(x)=4sin( ![]() x+
x+ ![]() )
)
D.f(x)=4sin( ![]() x+
x+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( ) 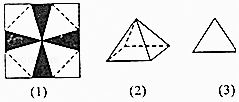
A.![]() cm3
cm3
B.![]() cm3
cm3
C.![]() cm3
cm3
D.![]() cm3
cm3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为2的正六边形ABCDEF中,动圆Q的半径为1,圆心在线段CD(含端点)上运动,P是圆Q上及内部的动点,设向量 ![]() (m,n为实数),则m+n的取值范围是( )
(m,n为实数),则m+n的取值范围是( )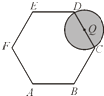
A.(1,2]
B.[5,6]
C.[2,5]
D.[3,5]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数x,y满足不等式组  ,若目标函数z=kx+y仅在点(1,1)处取得最小值,则实数k的取值范围是 ( )
,若目标函数z=kx+y仅在点(1,1)处取得最小值,则实数k的取值范围是 ( )
A.(﹣1,+∞)
B.(﹣∞,﹣1)
C.(1,+∞)
D.(﹣∞,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的面积(单位:cm2)等于( )
A.55π
B.75π
C.77π
D.65π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(3+x)﹣log2(3﹣x),
(1)求函数f(x)的定义域,并判断函数f(x)的奇偶性;
(2)已知f(sinα)=1,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年射阳县洋马镇政府决定投资8千万元启动“鹤乡菊海”观光旅游及菊花产业项目.规划从2017年起,在相当长的年份里,每年继续投资2千万元用于此项目.2016年该项目的净收入为5百万元(含旅游净收入与菊花产业净收入),并预测在相当长的年份里,每年的净收入均为上一年的1.5倍.记2016年为第1年,f(n)为第1年至此后第n(n∈N*)年的累计利润(注:含第n年,累计利润=累计净收入﹣累计投入,单位:千万元),且当f(n)为正值时,认为该项目赢利.
(1)试求f(n)的表达式;
(2)根据预测,该项目将从哪一年开始并持续赢利?请说明理由.
(参考数据: ![]() ,ln2≈0.7,ln3≈1.1)
,ln2≈0.7,ln3≈1.1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com