
已知函数 .
.
(Ⅰ)当 时,求证:函数
时,求证:函数 在
在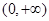 上单调递增;
上单调递增;
(Ⅱ)若函数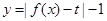 有三个零点,求
有三个零点,求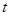 的值.
的值.
(I)利用导数法求解单调区间即可证明;(II)t=2
解析试题分析:(I)f’(x)=axlna+2x-lna=(ax-1) lna +2x
当a>1时,lna >0
当x∈(0,+∞)时,ax-1>0,2x>0
∴f’(x)>0,∴f(x)在(0,+∞)↑
(II)当a>1时,x∈(-∞,0)时,ax-1<0,2x<0
f’(x)<0,∴f(x)在(-∞,0)↓
当0<a<1时, x∈(0,+∞)时,lna <0, ax-1<0,
f’(x)>0,f(x)在(0,+∞)↑
x ∈(-∞,0)时, ax-1>0, lna <0
f’(x)<0, f(x)在(-∞,0)↓
∴当a>0且a≠1时,f(x) 在(-∞,0)↓,f(x)在(0,+∞)↑
∴x=0是f(x)在k上唯一极小值点,也是唯一最小值点.
f(x)min=f(0)=1
若y=[f(x)-t]-1有三个零点,即|f(x)-t|=1,f(x)=t±1有三个根,所以t+1>t-1
∴t-1="f" (x)min= 1,∴t=2
考点:本题考查了导数的运用
点评:导数本身是个解决问题的工具,是高考必考内容之一,高考往往结合函数甚至是实际问题考查导数的应用,求单调、最值、完成证明等,请注意归纳常规方法和常见注意点.


科目:高中数学 来源: 题型:解答题
已知f(x)= (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.
(1)求实数a的值组成的集合A;
(2)设关于x的方程f(x)= 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数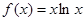 ,
,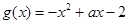
(1)求函数 在
在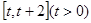 上的最小值;
上的最小值;
(2)若函数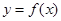 与
与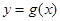 的图像恰有一个公共点,求实数a的值;
的图像恰有一个公共点,求实数a的值;
(3)若函数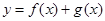 有两个不同的极值点
有两个不同的极值点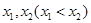 ,且
,且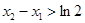 ,求实数a的取值范围。
,求实数a的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com