【题目】已知三棱锥
如图所示，其中
， 
，二面角
的大小为
.
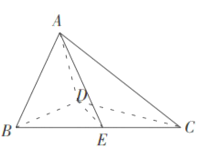
（1）证明： 
；
（2）若
为线段
的中点，且
， 
，求二面角
的余弦值.
应用题天天练四川大学出版社系列答案科目：高中数学 来源： 题型：
【题目】如图所示的几何体是圆柱的一部分，它是由矩形
（及其内部）以
边所在直线为旋转轴旋转
得到的，点
是弧
上的一点，点
是弧
的中点.
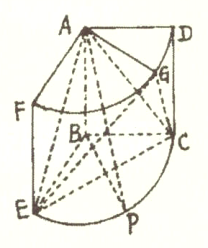
（1）求证：平面
平面
；
（2）当
且
时，求二面角
的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律：每生产产品
（百台），其总成本为
（万元），其中固定成本为2.8万元，并且每生产1百台的生产成本为1万元（总成本=固定成本+生产成本），销售收入
（万元）满足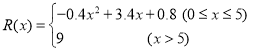
，假定该产品产销平衡（即生产的产品都能卖掉），根据上述统计规律，完成下列问题：
（1）写出利润函数
的解析式（利润=销售收入－总成本）；
（2）甲厂生产多少台产品时，可使盈利最多？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线
的焦点为
，直线
与抛物线
交于
两点．
（Ⅰ）若直线
过焦点
，且与圆
交于
（其中
在
轴同侧），求证： 
是定值；
（Ⅱ）设抛物线
在
和
点的切线交于点
，试问： 
轴上是否存在点
，使得
为菱形？若存在，请说明理由并求此时直线
的斜率和点
的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知f(x)＝
，x∈(－2，2)．
(1) 判断f(x)的奇偶性并说明理由；
(2) 求证：函数f(x)在(－2，2)上是增函数；
(3) 若f(2＋a)＋f(1－2a)>0，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某高校数学与统计学院为了对2018年录取的大一新生有针对性地进行教学.从大一新生中随机抽取40名，对他们在2018年高考的数学成绩进行调查，统计发现40名新生的数学分数
分布在
内.当
时，其频率
.
（Ⅰ）求
的值；
（Ⅱ）请在答题卡中画出这40名新生高考数学分数的频率分布直方图，并估计这40名新生的高考数学分数的平均数；
（Ⅲ）从成绩在100～120分的学生中，用分层抽样的方法从中抽取5名学生，再从这5名学生中随机选两人甲、乙，记甲、乙的成绩分别为
，求概率
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝1－
(a>0，a≠1)且f(0)＝0.
(1)求a的值；
(2)若函数g(x)＝(2x＋1)·f(x)＋k有零点，求实数k的取值范围；
(3)当x∈(0，1)时，f(x)>m·2x－2恒成立，求实数m的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
