
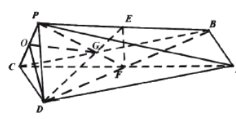
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形,![]() ,
,![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,设
,设![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)利用线面平行的性质定理即可得到结论;
(2)方法一:利用几何法求线面角,一作,二证,三求解;方法二:利用空间直角坐标系,线面角的向量关系即可得到结论.
(1)解析:因为底面![]() 为平行四边形,
为平行四边形,![]() 是
是![]() 中点,所以
中点,所以![]() 是
是![]() 中点,所以
中点,所以![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)解析1:(几何法)
因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以直线![]() 与平面
与平面![]() 的交点即为
的交点即为![]() 与
与![]() 的交点,设为
的交点,设为![]() ,
,
![]() ,所以
,所以![]() 为等边三角形,取
为等边三角形,取![]() 中点
中点![]() ,
,
则![]() ,因为
,因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() 是直线
是直线![]() 与平面
与平面![]() 所成角,
所成角,
因为![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,所以
的中点,所以![]() 是
是![]() 的重心,
的重心,
在![]() 中,
中,![]() ,所以
,所以![]() ,在平行四边形
,在平行四边形![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,所以
,所以![]() ,
,
所以![]() ,又因为
,又因为![]() ,
,
所以![]() ,即直线
,即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
解析2:(向量法)
取![]() 中点
中点![]() ,则
,则![]() ,因为
,因为![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() ,所以
,所以![]() 为等边三角形,
为等边三角形,
所以![]() ,此时
,此时![]() ,
,![]() ,
,![]() 两两垂直,
两两垂直,
如图,建立空间直角坐标系,![]() ,
,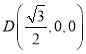 ,
,
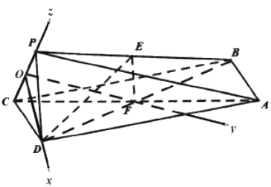
在![]() 中,
中,![]() ,所以
,所以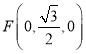 ,由
,由![]() ,得
,得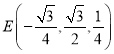 ,
,
所以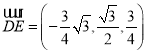 ,平面
,平面![]() 的法向量为
的法向量为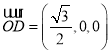 ,
,
所以 ,
,
所以![]() ,
,
即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】图(![]() )是某品牌汽车
)是某品牌汽车![]() 年月销量统计图,图(
年月销量统计图,图(![]() )是该品牌汽车月销量占所属汽车公司当月总销量的份额统计图,则下列说法错误的是( )
)是该品牌汽车月销量占所属汽车公司当月总销量的份额统计图,则下列说法错误的是( )
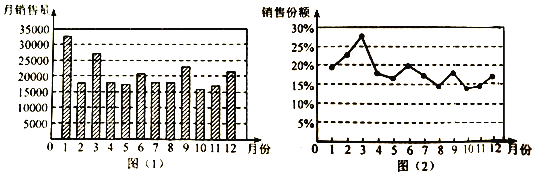
A.该品牌汽车![]() 年全年销量中,
年全年销量中,![]() 月份月销量最多
月份月销量最多
B.该品牌汽车![]() 年上半年的销售淡季是
年上半年的销售淡季是![]() 月份,下半年的销售淡季是
月份,下半年的销售淡季是![]() 月份
月份
C.![]() 年该品牌汽车所属公司
年该品牌汽车所属公司![]() 月份的汽车销量比
月份的汽车销量比![]() 月份多
月份多
D.该品牌汽车![]() 年下半年月销量相对于上半年,波动性小,变化较平稳
年下半年月销量相对于上半年,波动性小,变化较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() ,定义
,定义![]() 为数列
为数列![]() 的一阶差分数列,其中
的一阶差分数列,其中![]() .
.
(1)若![]() ,试判断
,试判断![]() 是否是等差数列,并说明理由;
是否是等差数列,并说明理由;
(2)若![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)对(2)中的数列![]() ,是否存在等差数列
,是否存在等差数列![]() ,使得
,使得![]() 对一切
对一切![]() 都成立,若存在,求出数列
都成立,若存在,求出数列![]() 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 对任意的
对任意的![]() ,都有
,都有![]()
![]() ,且
,且![]() ,则称数列
,则称数列![]() 为“k级创新数列”.
为“k级创新数列”.
(1)已知数列![]() 满足
满足![]() 且
且![]() ,试判断数列
,试判断数列![]() 是否为“2级创新数列”,并说明理由;
是否为“2级创新数列”,并说明理由;
(2)已知正数数列![]() 为“k级创新数列”且
为“k级创新数列”且![]() ,若
,若![]() ,求数列
,求数列![]() 的前n项积
的前n项积![]() ;
;
(3)设![]() ,
,![]() 是方程
是方程![]() 的两个实根
的两个实根![]() ,令
,令![]() ,在(2)的条件下,记数列
,在(2)的条件下,记数列![]() 的通项
的通项![]() ,求证:
,求证:![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinx-xcosx-x,f′(x)为f(x)的导数.
(1)证明:f′(x)在区间(0,π)存在唯一零点;
(2)若x∈[0,π]时,f(x)≥ax,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线的中心在原点,焦点F1、F2在坐标轴上,焦距是实轴长的![]() 倍且过点(4,﹣
倍且过点(4,﹣![]() )
)
(1)求双曲线方程;
(2)若点M(3,m)在双曲线上,求证:点M在以F1F2为直径的圆上;
(3)在(2)条件下,若M F2交双曲线另一点N,求△F1MN的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】蚂蚁森林是支付宝客户端为首期“碳账户”设计的一款公益行动:用户通过步行、地铁出行、在线缴纳水电煤气费、网络挂号、网络购票等行为就会减少相应的碳排放量,可以用来在支付宝里养一棵虚拟的树.这棵树长大后,公益组织、环保企业等蚂蚁生态伙伴们可以在现实沙漠化地区(阿拉善、通辽、库布齐等)种下一棵实体的树目前通辽地区对部分基地樟子松幼苗的培育技术进行了改进,为了了解改进后的效果,现从改进前后的树苗培育基地各抽取了![]() 株产品作为样本,检测其同样生长周期的高度(单位:
株产品作为样本,检测其同样生长周期的高度(单位:![]() ),若高度不低于
),若高度不低于![]() 才适合移植,否则继续等待生长图1是改进前的样本的频率分布直方图,表2是改进后的样本频率分布表.
才适合移植,否则继续等待生长图1是改进前的样本的频率分布直方图,表2是改进后的样本频率分布表.
图1
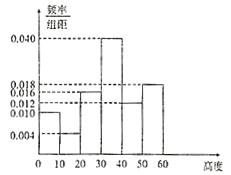
表2技术改进后样本的频率分布表
高度 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据图1和表2提供的信息,试从移植率的角度对培育技术改进前后的优劣进行比较;
(2)估计培育技术未改进的基地树苗高度的平均数;
(3)在市场中,规定高度在![]() 内的为三等苗,
内的为三等苗,![]() 内的为二等苗,
内的为二等苗,![]() 内的为一等苗.现从表2高度不低于
内的为一等苗.现从表2高度不低于![]() 的树苗样本中采用分层抽样的方法抽取
的树苗样本中采用分层抽样的方法抽取![]() 株,再从这
株,再从这![]() 株幼苗中随机抽取
株幼苗中随机抽取![]() 株,求这
株,求这![]() 株中一、二、三等苗都有的概率.
株中一、二、三等苗都有的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com