考点:函数奇偶性的判断,函数的值域
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:(1)解出
2x=,令2
x>0,解出即可得到值域;
(2)运用单调性的定义判断,注意作差、变形、定符号、下结论等步骤;
(3)运用奇偶性的定义,注意先求定义域,再计算f(-x);
(4)先由奇偶性得到f(1-m)<f(m
2-1),再运用单调性得到1-m<m
2-1,解出即可.
解答:
解:(1)∵
2x=,
又2
x>0,∴-1<y<1.
∴函数f(x)的值域为(-1,1);
(2)函数f(x)在R上为单调增函数.
证明:
f(x)==
1-在定义域R中任取两个实数x
1,x
2,且x
1<x
2,
则
f(x1)-f(x2)=.
∵x
1<x
2,∴0<2
x1<2
x2,
从而f(x
1)-f(x
2)<0.
∴函数f(x)在R上为单调增函数.
(3)函数f(x)为奇函数.
证明:定义域为R,关于原点对称,
∵
f(-x)===-f(x),
∴函数f(x)为奇函数;
(4)∴f(1-m)+f(1-m
2)<0即f(1-m)<-f(1-m
2),
∴f(1-m)<f(m
2-1),
由于函数f(x)在R上为单调增函数,
则1-m<m
2-1,即m
2+m-2>0,解得m<-2或m>1.
∴原不等式的解集为(-∞,-2)∪(1,+∞).
点评:本题考查函数的性质和运用,考查函数的单调性的判断,以及函数的奇偶性的判断,注意运用定义,同时考查二次不等式的解法,属于中档题.



 阅读快车系列答案
阅读快车系列答案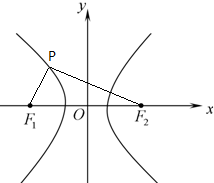 如图,若F1,F2是双曲线
如图,若F1,F2是双曲线