
【题目】若函数exf(x)(e=2.71828…,是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质,下列函数:
①f(x)=![]() (x>1) ②f(x)=x2 ③f(x)=cosx ④f(x)=2-x
(x>1) ②f(x)=x2 ③f(x)=cosx ④f(x)=2-x
中具有M性质的是__________.
 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:
【题目】在数列{an},{bn}中,a1=2,b1=4且an , bn , an+1成等差数列,bn , an+1 , bn+1成等比数列(n∈N*)
(1)求a2 , a3 , a4及b2 , b3 , b4;由此归纳出{an},{bn}的通项公式,并证明你的结论.
(2)若cn=log2(![]() ),Sn=c1+c2+…+cn , 试问是否存在正整数m,使Sm≥5,若存在,求最小的正整数m.
),Sn=c1+c2+…+cn , 试问是否存在正整数m,使Sm≥5,若存在,求最小的正整数m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , a1=1,且nan+1=2Sn(n∈N*),数列{bn}满足b1=![]() , b2=
, b2=![]() , 对任意n∈N* , 都有bn+12=bnbn+2 .
, 对任意n∈N* , 都有bn+12=bnbn+2 .
求数列{an}、{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
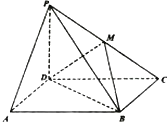
(1)求证:AP∥平面MBD;
(2)若AD⊥PB,求证:BD⊥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C: ![]() ,直线l:
,直线l: ![]()

(Ⅰ)求直线l所过定点A的坐标;
(Ⅱ)求直线l被圆C所截得的弦长最短时m的值及最短弦长;
(Ⅲ)已知点![]() ,在直线MC上(C为圆心),存在定点N(异于点M),满足:对于圆C上任一点P,都有
,在直线MC上(C为圆心),存在定点N(异于点M),满足:对于圆C上任一点P,都有![]() 为一常数,试求所有满足条件的点N的坐标及该常数。
为一常数,试求所有满足条件的点N的坐标及该常数。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)=(2x-x2)ex
①(-![]() ,
,![]() )是f(x)的单调递减区间;
)是f(x)的单调递减区间;
②f(-![]() )是f(x)的极小值,f(
)是f(x)的极小值,f(![]() )是f(x)的极大值;
)是f(x)的极大值;
③f(x)没有最大值,也没有最小值;
④f(x)有最大值,没有最小值.
其中判断正确的是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列向量组中,可以把向量![]() =(3,2)表示出来的是( )
=(3,2)表示出来的是( )
A.![]() =(0,0),
=(0,0),![]() =(1,2)
=(1,2)
B.![]() =(﹣1,2),
=(﹣1,2),![]() =(5,﹣2)
=(5,﹣2)
C.![]() =(3,5),
=(3,5),![]() =(6,10)
=(6,10)
D.![]() =(2,﹣3),
=(2,﹣3), ![]() =(﹣2,3)
=(﹣2,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com