[题目]已知函数的定义域为.对于任意实数..都有.当时..(1)求的值,(2)证明:当时..(3)证明:在上单调递减.(4)若对任意恒成立.求实数的取值范围. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知函数的定义域为，对于任意实数，，都有，当时，.

（1）求的值；

（2）证明：当时，.

（3）证明：在上单调递减.

（4）若对任意恒成立，求实数的取值范围.

【答案】（1）；（2）证明见解析；（3）证明见解析；（4）.

【解析】

（1）令，，化简后可得的值.

（2）设，由题设可得，从而得到，结合可得.

（3）利用单调性的定义可证在上单调递减.

（4）原不等式等价于，利用单调性和（1）中的结论可得对任意的恒成立，参变分离后可求的取值范围.

（1）令，，∴，

∵时，，∴，∴.

（2）设，，则，

∴，∵，∴，即.

（3）任取，且，

则

，

∵，∴，∴，

又∵，∴，即，

∴，∴在上单调递减.

（4），∴，

令,则，故在上恒成立，

所以在上恒成立，

由基本不等式可得，当且仅当等号成立，

故即.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】某校响应教育部门疫情期间“停课不停学”的号召，实施网络授课，为检验学生上网课的效果，高三学年进行了一次网络模拟考试.全学年共1500人，现从中抽取了100人的数学成绩，绘制成频率分布直方图(如图所示).已知这100人中分数段的人数比分数段的人数多6人.

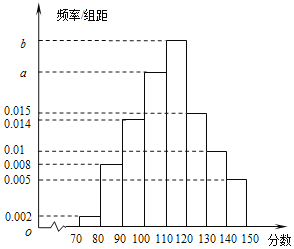
（1）根据频率分布直方图，求a，b的值，并估计抽取的100名同学数学成绩的中位数；(中位数保留两位小数)

（2）现用分层抽样的方法从分数在，的两组同学中随机抽取6名同学，从这6名同学中再任选2名同学作为“网络课堂学习优秀代表”发言，求这2名同学的分数不在同一组内的概率.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】选修4-4：坐标系与参数方程

在直角坐标系中，直线的参数方程为（为参数），在以原点为极点，轴正半轴为极轴的极坐标系中，圆的方程为．

（1）写出直线的普通方程和圆的直角坐标方程；

（2）设点，直线与圆相交于两点，求的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在班级活动中，4名男生和3名女生站成一排表演节目：（写出必要的数学式，结果用数字作答）

（1）三名女生不能相邻，有多少种不同的站法？

（2）四名男生相邻有多少种不同的排法？

（3）女生甲不能站在左端，女生乙不能站在右端，有多少种不同的排法？

（4）甲乙丙三人按高低从左到右有多少种不同的排法？（甲乙丙三位同学身高互不相等）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】秸秆还田是当今世界上普通重视的一项培肥地力的增产措施，在杜绝了秸秆焚烧所造成的大气污染的同时还有增肥增产作用．某农机户为了达到在收割的同时让秸秆还田，花元购买了一台新型联合收割机，每年用于收割可以收入万元（已减去所用柴油费）；该收割机每年都要定期进行维修保养，第一年由厂方免费维修保养，第二年及以后由该农机户付费维修保养，所付费用（元）与使用年数的关系为：，已知第二年付费元，第五年付费元．