练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本小题满分14分）
    在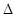ABC中，BC=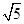，AC=3，sinC="2sinA"
    （I）求AB的值：
    (II) 求sin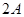的值.

    （Ⅰ）AB=；（Ⅱ）sin2A=2sinAcosA=。

    解析试题分析：（I）由正弦定理可求出AB.
    (II)由余弦定理可求出cosA,然后再利用求出sinA.
    （Ⅰ）解：在△ABC中，根据正弦定理，
    于是AB=　．．．．．．．．．．．．．．７分
    （Ⅱ）解：在△ABC中，根据余弦定理，得cosA=　．．．．．．．．．．．．．．．．．．１２分
    sinA=　　从而　sin2A=2sinAcosA=　．．．　（14分）
    考点：正余弦定理在解三角形当中的应用，同角三角函数的基本关系式.
    点评：解本小题用到的公式有：;
    .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    (本小题12分) =（）， =，f（x）=
    ①求f(x)图象对称中心坐标
    ②若△ABC三边a、b、c满足b2=ac，且b边所对角为x，求x的范围及f（x）值域。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设函数
    （1）设的内角，且为钝角，求的最小值；
    （2）设是锐角的内角，且求的三个内角的大小和AC边的长。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    本小题满分10分）
    在△ABC中，A、B为锐角，角A、B、C所对的边分别为、、，且，。
    (1)求角C的值；      
    (2)若a－b＝－1，求、、的值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    (本题满分12 分)
    如图，从气球上测得正前方的河流的两岸的俯角分别为，如果这时气球的高度米，求河流的宽度.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本题满分12分）已知、、分别是的三个内角、、所对的边；
    （1）若面积，且、、成等差数列，求、的值；
    （2）若，且，试判断的形状。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分10分）
    在中，角所对的边分别是，且满足，．
    （Ⅰ）求的值；
    （Ⅱ）设，求的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题12分）ΔABC中A,B,C的对边分别为a,b,c，且
    求：（1）角B的大小；   （2）若，求ΔABC的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （10分）在△ABC中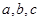，分别为内角A.B.C所对的边，且满足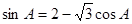
    （1）求角A的大小
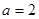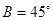    （2）现给出三个条件：①②③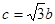试从中选出两个可以确定△ABC的条件写出你的选择，并以此为依据求△ABC的面积（只需写出一个选定方案即可，选多种方案以第一种方案记分）

    查看答案和解析>>

    同步练习册答案