
【题目】已知圆M的圆心在直线x﹣2y+4=0上,且与x轴交于两点A(﹣5,0),B(1,0). (Ⅰ)求圆M的方程;
(Ⅱ)求过点C(1,2)的圆M的切线方程;
(Ⅲ)已知D(﹣3,4),点P在圆M上运动,求以AD,AP为一组邻边的平行四边形的另一个顶点Q轨迹方程.
【答案】解:(Ⅰ)∵圆M与x轴交于两点A(﹣5,0)、B(1,0), ∴圆心在AB的垂直平分线上,即C在直线x=﹣2上.
由 ![]() ,解得
,解得 ![]() ,即圆心M的坐标为(﹣2,1).
,即圆心M的坐标为(﹣2,1).
∴半径 ![]() ,
,
因此,圆M的方程为(x+2)2+(y﹣1)2=10.
(Ⅱ)∵点C(1,2)满足(1+2)2+(2﹣1)2=10,
∴点C在圆M上,可得经过点C与圆M相切的直线与CM垂直.
∵CM的斜率kCM= ![]() ,∴过点C的切线斜率为k=
,∴过点C的切线斜率为k= ![]() =﹣3,
=﹣3,
由此可得过点C(1,2)的圆M的切线方程为y﹣2=﹣3(x﹣1),化简得3x+y﹣5=0.
(Ⅲ)设Q(x,y)、P(x0 , y0),
∵四边形ADQP为平行四边形,∴对角线AQ、PD互相平分,即AQ的中点也是PD的中点.
即 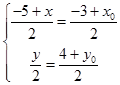 ,解得
,解得 
将P(x﹣2,y﹣4)代入圆M的方程,可得(x﹣2+2)2+(y﹣4﹣1)2=10,即x2+(y﹣5)2=10,
∴顶点Q在圆x2+(y﹣5)2=10上运动,
∵圆x2+(y﹣5)2=10交直线AD于点(﹣1,8)和(﹣3,4),
当Q与这两个点重合时,不能构成平行四边形ADQP,
∴顶点Q的轨迹方程为x2+(y﹣5)2=10,(点(﹣1,8)、(﹣3,4)除外)
【解析】(Ⅰ)根据圆的性质,可得圆心M为AB垂直平分线与直线x﹣2y+4=0的交点.因此联解两直线的方程,得到圆心M的坐标,由两点的距离公式算出半径r= ![]() ,即可得到圆M的方程;(Ⅱ)由于点C是圆M上的点,所以过点C的圆M的切线与CM垂直.因此利用直线的斜率公式算出CM的斜率,从而得到切线的斜率k=﹣3,根据直线方程的点斜式列式,化简即得所求切线的方程;(Ⅲ)设Q(x,y)、P(x0 , y0),根据平行四边形ADQP的对角线互相平分,利用线段的中点坐标公式列式,解出P的坐标为(x﹣2,y﹣4),代入圆M的方程化简可得x2+(y﹣5)2=10.最后根据构成平行四边形的条件,去除两个杂点(﹣1,8)、(﹣3,4),即可得到顶点Q的轨迹方程.
,即可得到圆M的方程;(Ⅱ)由于点C是圆M上的点,所以过点C的圆M的切线与CM垂直.因此利用直线的斜率公式算出CM的斜率,从而得到切线的斜率k=﹣3,根据直线方程的点斜式列式,化简即得所求切线的方程;(Ⅲ)设Q(x,y)、P(x0 , y0),根据平行四边形ADQP的对角线互相平分,利用线段的中点坐标公式列式,解出P的坐标为(x﹣2,y﹣4),代入圆M的方程化简可得x2+(y﹣5)2=10.最后根据构成平行四边形的条件,去除两个杂点(﹣1,8)、(﹣3,4),即可得到顶点Q的轨迹方程.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设实数a∈R,函数 ![]() 是R上的奇函数. (Ⅰ)求实数a的值;
是R上的奇函数. (Ⅰ)求实数a的值;
(Ⅱ)当x∈(1,1)时,求满足不等式f(1m)+f(1m2)<0的实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg ![]() (a>0)为奇函数,函数g(x)=
(a>0)为奇函数,函数g(x)= ![]() +b(b∈R).
+b(b∈R).
(Ⅰ)求a;
(Ⅱ)若b>1,讨论方徎g(x)=ln|x|实数根的个数;
(Ⅲ)当x∈[ ![]() ,
, ![]() ]时,关于x的不等式f(1﹣x)≤log(x)有解,求b的取值范围.
]时,关于x的不等式f(1﹣x)≤log(x)有解,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为2的正方体内有一四面体A﹣BCD,其中B,C分别为正方体两条棱的中点,其三视图如图所示,则四面体A﹣BCD的体积为( ) 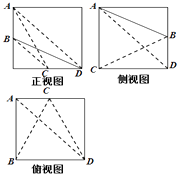
A.![]()
B.2
C.![]()
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为 ![]() ,
, ![]() ,f3(x)=x,f4(x)=log2(x+1),有以下结论: ①当x>1时,甲走在最前面;
,f3(x)=x,f4(x)=log2(x+1),有以下结论: ①当x>1时,甲走在最前面;
②当x>1时,乙走在最前面;
③当0<x<1时,丁走在最前面,当x>1时,丁走在最后面;
④丙不可能走在最前面,也不可能走在最后面;
⑤如果它们一直运动下去,最终走在最前面的是甲.
其中,正确结论的序号为(把正确结论的序号都填上,多填或少填均不得分).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ln(1﹣ ![]() )+1,则f(﹣7)+f(﹣5 )+f(﹣3)+f(﹣1)+f(3 )+f( 5)+f(7 )+f( 9)=( )
)+1,则f(﹣7)+f(﹣5 )+f(﹣3)+f(﹣1)+f(3 )+f( 5)+f(7 )+f( 9)=( )
A.0
B.4
C.8
D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=2sin(180°﹣x)+cos(﹣x)﹣sin(450°﹣x)+cos(90°+x).
(1)若f(α)= ![]() α∈(0°,180°),求tanα;
α∈(0°,180°),求tanα;
(2)若f(α)=2sinα﹣cosα+ ![]() ,求sinαcosα的值.
,求sinαcosα的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com