
【题目】已知![]() ,
, ![]() 分别是椭圆
分别是椭圆![]() :
: ![]() (
(![]() )的左、右焦点,离心率为
)的左、右焦点,离心率为![]() ,
, ![]() ,
, ![]() 分别是椭圆的上、下顶点,
分别是椭圆的上、下顶点, ![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 作直线
作直线![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点,求三角形
两点,求三角形![]() 面积的最大值(
面积的最大值(![]() 是坐标原点).
是坐标原点).
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据离心率为![]() ,
, ![]() ,列出关于
,列出关于![]() 、
、![]() 、
、![]() 的方程组,结合性质
的方程组,结合性质![]() ,求出
,求出![]() 、
、![]() 、
、![]() ,即可得椭圆
,即可得椭圆![]() 的方程;(2)直线
的方程;(2)直线![]() 斜率存在,设其方程为
斜率存在,设其方程为![]() .,直线方程与椭圆方程联立,根据韦达定理,弦长公式、点到直线距离公式及三角形面积公式将角形
.,直线方程与椭圆方程联立,根据韦达定理,弦长公式、点到直线距离公式及三角形面积公式将角形![]() 面积用
面积用![]() 表示,利用基本不等式 即可得结果.
表示,利用基本不等式 即可得结果.
试题解析:(1)由题知, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,∴
,∴![]() ,①
,①
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,②
,②
①②联立解得![]() ,
, ![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
, ![]() ,显然直线
,显然直线![]() 斜率存在,设其方程为
斜率存在,设其方程为![]() ,
,
代入![]() ,整理得
,整理得![]() ,
,
则![]() ,即
,即![]() ,
, ![]() ,
, ![]() ,
,
![]()
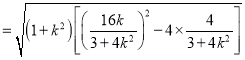
 ,
,
所以![]() 到
到![]() 的距离
的距离![]() ,
,
所以三角形![]() 面积
面积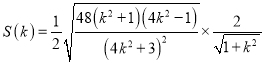
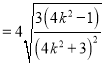 ,
,
设![]() ,所以
,所以 ,
,
当且仅当![]() ,即
,即![]() ,即
,即![]() ,即
,即![]() 时取等号,
时取等号,
所以![]() 面积的最大值为
面积的最大值为![]() .
.
【方法点晴】本题主要考查待定系数法求椭圆方程及圆锥曲线求最值,属于难题.解决圆锥曲线中的最值问题一般有两种方法:一是几何意义,特别是用圆锥曲线的定义和平面几何的有关结论来解决,非常巧妙;二是将圆锥曲线中最值问题转化为函数问题,然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法,本题(2)就是用的这种思路,利用均值不等式法求三角形最值的.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】对某电子元件进行寿命追踪调查,情况如下.
寿命(h) | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
个 数 | 20 | 30 | 80 | 40 | 30 |
(1)列出频率分布表;
(2)画出频率分布直方图;
(3)估计元件寿命在100~400h以内的在总体中占的比例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的左、右焦点分别为F1、F2 , 短轴两个端点为A、B,且四边形F1AF2B是边长为2的正方形.
的左、右焦点分别为F1、F2 , 短轴两个端点为A、B,且四边形F1AF2B是边长为2的正方形. 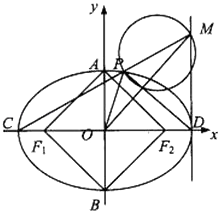
(1)求椭圆的方程;
(2)若C、D分别是椭圆长的左、右端点,动点M满足MD⊥CD,连接CM,交椭圆于点P.证明: ![]() 为定值.
为定值.
(3)在(2)的条件下,试问x轴上是否存异于点C的定点Q,使得以MP为直径的圆恒过直线DP、MQ的交点,若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家举行大型的促销活动,经测算某产品当促销费用为![]() 万元时,销售量
万元时,销售量![]() 万件满足
万件满足![]() (其中
(其中![]() ,
, ![]() 为正常数),现假定生产量与销售量相等,已知生产该产品
为正常数),现假定生产量与销售量相等,已知生产该产品![]() 万件还需投入成本
万件还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为![]() 万元/万件.
万元/万件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国许多省市雾霾天气频发,为增强市民的环境保护意识,某市面向全市征召![]() 名义务宣传志愿者,成立环境保护宣传组织,现把该组织的成员按年龄分成
名义务宣传志愿者,成立环境保护宣传组织,现把该组织的成员按年龄分成![]() 组第
组第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示,已知第
,得到的频率分布直方图如图所示,已知第![]() 组有
组有![]() 人.
人.

(1)求该组织的人数;
(2)若在第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 名志愿者参加某社区的宣传活动,应从第
名志愿者参加某社区的宣传活动,应从第![]() 组各抽取多少名志愿者?
组各抽取多少名志愿者?
(3)在(2)的条件下,该组织决定在这![]() 名志愿者中随机抽取
名志愿者中随机抽取![]() 名志愿者介绍宣传经验,求第
名志愿者介绍宣传经验,求第![]() 组至少有
组至少有![]() 名志愿者被抽中的概率.
名志愿者被抽中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com