
分析 半径为8的半圆的弧长是8π,圆锥的底面周长等于侧面展开图的扇形弧长,因而圆锥的底面周长是8π,利用弧长公式计算,求出半径,进而可得高,即可求出圆锥的体积.
解答 解:∵圆锥的侧面展开图是一个半径为8的半圆,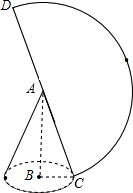
∴圆锥的母线长为8,
设圆锥的底面半径为r,
则2πr=π×8,
∴r=4.
圆锥的高为:$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
∴圆锥的体积=$\frac{1}{3}$π•42•4$\sqrt{3}$=$\frac{64\sqrt{3}}{3}$π.
故答案为:$\frac{64\sqrt{3}}{3}$π.
点评 本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长,正确对这两个关系的记忆是解题的关键


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:解答题
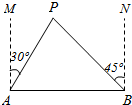 如图,A、B两座城市相距100千米,现计划在这两座城市之间修筑一条高等级公路(即线段AB).经测量,森林保护区中心P点在A城市的北偏东30°方向,B城市的北偏西45°方向上,已知森林保护区的范围在以P为圆心,50千米为半径的圆形区域内.请问:计划修筑的这条高等级公路会不会穿越保护区,为什么?
如图,A、B两座城市相距100千米,现计划在这两座城市之间修筑一条高等级公路(即线段AB).经测量,森林保护区中心P点在A城市的北偏东30°方向,B城市的北偏西45°方向上,已知森林保护区的范围在以P为圆心,50千米为半径的圆形区域内.请问:计划修筑的这条高等级公路会不会穿越保护区,为什么?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-3<x<2} | B. | {x|-3<x<1} | C. | {x|1<x<2} | D. | {x|2<x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
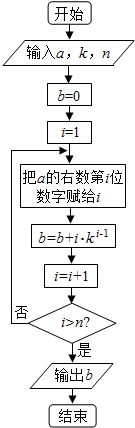
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com