
【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数.
是奇函数.
(1)求![]() 的值;
的值;
(2)猜测![]() 的单调性,并用定义证明;
的单调性,并用定义证明;
(3)若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)减函数;(3)
;(2)减函数;(3)![]()
【解析】试题分析:根据函数为奇函数,利用奇函数的定义和函数定义域中含有x=0,f(0)=0,列方程组解出参数a,b,写出函数的解析式;分离常数容易猜出函数为减函数,用定义法证明函数的单调性,步骤为①取值,②作差,③变形,④断号,最后给出单调性结论.恒成立问题,采用分离参数,求最值,借助“极值原理”求出参数的范围
试题解析:
(1)由![]() ,可得
,可得![]() ,检验:当
,检验:当![]() 时,
时, ![]() ,定义域为
,定义域为![]() ,对任意
,对任意![]() ,都有
,都有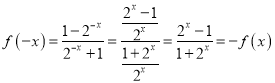 ,所以
,所以![]() 为奇函数.
为奇函数.
(2)![]() 在
在![]() 单调递减. 以下用定义证明:设
单调递减. 以下用定义证明:设![]() ,则
,则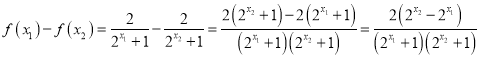 ,因为函数
,因为函数![]() 在
在![]() 为增函数,且
为增函数,且![]() ,所以
,所以![]() .又因为
.又因为![]() ,所以
,所以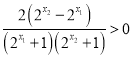 ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 单调递减.
单调递减.
(3)由![]() 可得
可得![]() ,因为
,因为![]() 在
在![]() 单调递减,所以任意
单调递减,所以任意![]() ,都有
,都有![]() 恒成立,若
恒成立,若![]() ,则
,则![]() ,符合题意,所以
,符合题意,所以![]() ;若
;若![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,若
,若![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,综上所述,实数
,综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知集合P={x|-2≤x≤10},Q={x|1-m≤x≤1+m}.
(1)求集合RP;
(2)若PQ,求实数m的取值范围;
(3)若P∩Q=Q,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校大一新生中的6名同学打算参加学校组织的“演讲团”、“吉他协会”等五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中没有人参加“演讲团”的不同参加方法数为( )
A. 3600 B. 1080 C. 1440 D. 2520
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(Ⅱ)设![]() ,
,![]() ,(
,(![]() 为自然对数的底数).是否存在常数
为自然对数的底数).是否存在常数![]() ,使
,使![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
(Ⅰ)应收集多少位女生样本数据?
(Ⅱ)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() .估计该校学生每周平均体育运动时间超过4个小时的概率.
.估计该校学生每周平均体育运动时间超过4个小时的概率.
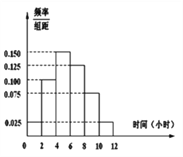
(Ⅲ)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有![]() 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附:
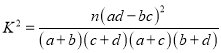
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域是R,对于任意实数
的定义域是R,对于任意实数![]() ,恒有
,恒有![]() ,且当
,且当![]() 时,
时, ![]() 。
。
(1)求证: ![]() ,且当
,且当![]() 时,有
时,有![]() ;
;
(2)判断![]() 在R上的单调性;
在R上的单调性;
(3)设集合A=![]() ,B=
,B=![]() ,若A∩B=
,若A∩B=![]() ,求
,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为![]() ,边界忽略不计)即为中奖·
,边界忽略不计)即为中奖·
乙商场:从装有2个白球、2个蓝球和2个红球的盒子中一次性摸出1球(这些球除颜色外完全相同),它是红球的概率是![]() ,若从盒子中一次性摸出2球,且摸到的是2个相同颜色的球,即为中奖.
,若从盒子中一次性摸出2球,且摸到的是2个相同颜色的球,即为中奖.

(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)试问:购买该商品的顾客在哪家商场中奖的可能性大?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com