
【题目】在数列{an}中,a1=1,an+1=2an+2n .
(1)设bn= ![]() ,证明:数列{bn}是等差数列.
,证明:数列{bn}是等差数列.
(2)求数列{an}的前n项和.
【答案】
(1)证明:∵an+1=2an+2n,∴ ![]() ,
,
∴bn+1﹣bn=1.
∴数列{bn}是等差数列,首项为 ![]() =1,公差为1
=1,公差为1
(2)解:由(1)可得:bn=1+(n﹣1)=n,
∴ ![]() ,
,
∴ ![]() ,
,
∴数列{an}的前n项和Sn=1+2×2+3×22+…+n2n﹣1,
2Sn=2+2×22+3×23+…+(n﹣1)×2n﹣1+n×2n,
∴﹣Sn=1+2+22+…+2n﹣1﹣n×2n= ![]() ﹣n×2n=(1﹣n)×2n﹣1.
﹣n×2n=(1﹣n)×2n﹣1.
∴Sn=(n﹣1)×2n+1
【解析】(1)由an+1=2an+2n , 可得 ![]() ,即bn+1﹣bn=1.即可证明;(2)由(1)可得:bn=1+(n﹣1)=n,
,即bn+1﹣bn=1.即可证明;(2)由(1)可得:bn=1+(n﹣1)=n, ![]() ,再利用“错位相减法”、等比数列的前n项和公式即可得出.
,再利用“错位相减法”、等比数列的前n项和公式即可得出.
【考点精析】利用等差关系的确定和数列的前n项和对题目进行判断即可得到答案,需要熟知如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么这个数列就叫做等差数列;数列{an}的前n项和sn与通项an的关系
)那么这个数列就叫做等差数列;数列{an}的前n项和sn与通项an的关系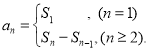 .
.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】给定两个命题,P:对任意实数x都有ax2+ax+1>0恒成立;Q:关于x的方程x2﹣x+a=0有实数根;如果P与Q中有且仅有一个为真命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC是斜三角形,内角A、B、C所对的边的长分别为a、b、c.若csinA= ![]() acosC.
acosC.
(1)求角C;
(2)若c= ![]() ,且sinC+sin(B﹣A)=5sin2A,求△ABC的面积.
,且sinC+sin(B﹣A)=5sin2A,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是一个公差大于0的等差数列,且满足![]() ,a2+a7=16
,a2+a7=16
(1)求数列{an}的通项公式;
(2)数列{an}和数列{bn}满足等式![]() (n∈N*),求数列{bn}的前n项和Sn.
(n∈N*),求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设![]() 与定点
与定点![]() 的距离和它到直线
的距离和它到直线![]() 的距离的比是常数
的距离的比是常数![]() ,
,
(1)求点![]() 的轨迹曲线
的轨迹曲线![]() 的方程:
的方程:
(2)过定点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,以
两点,以![]() 三点(
三点(![]() 为坐标原点)为顶点作平行四边形
为坐标原点)为顶点作平行四边形![]() ,若点
,若点![]() 刚好在曲线
刚好在曲线![]() 上,求直线
上,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四棱锥(底面为正方形,顶点在底面上的射影是底面的中心)S﹣ABCD的底面边长为2,高为2,E为边BC的中点,动点P在表面上运动,并且总保持PE⊥AC,则动点P的轨迹的周长为( )
A.![]()
B.![]()
C.3 ![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为![]() 的圆形纸板内有一个相同圆心的半径为
的圆形纸板内有一个相同圆心的半径为![]() 的小圆,现将半径为
的小圆,现将半径为![]() 的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( )
的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知 ![]() tanAtanB﹣tanA﹣tanB=
tanAtanB﹣tanA﹣tanB= ![]() .
.
(1)求∠C的大小;
(2)设角A,B,C的对边依次为a,b,c,若c=2,且△ABC是锐角三角形,求a2+b2的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com