
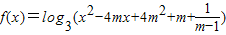 ,其中m是实数,设M={m|m>1}
,其中m是实数,设M={m|m>1}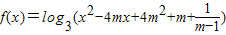 ,
,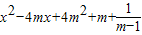
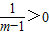 ,∴t>0.
,∴t>0. )=
)=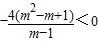 ,
, )2+
)2+ >0,
>0,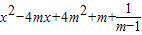
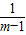 ≥m+
≥m+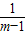 ,(x=2m时取等号).
,(x=2m时取等号).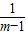 ).
).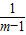 =m-1+
=m-1+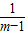 +1,
+1,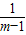 +1≥3,当且仅当m-1=
+1≥3,当且仅当m-1=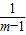 ,即m=2时取等号.
,即m=2时取等号.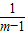 )≥1,
)≥1,

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
| 1 | m-1 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高三回头考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)设函数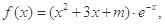 (其中
(其中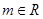 ,
,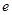 是自然对数的底数)
是自然对数的底数)
(I)若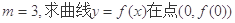 处的切线方程;
处的切线方程;
(II)若函数 上有两个极值点.
上有两个极值点.
①求实数m的范围; ②证明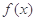 的极小值大于e.
的极小值大于e.
查看答案和解析>>
科目:高中数学 来源:2014届广东省高一下学期期中数学试卷(解析版) 题型:解答题
已知函数 ,其中m是实数
,其中m是实数
(1)若函数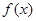 有零点,求m的取值范围;(7分)
有零点,求m的取值范围;(7分)
(2)设不等式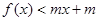 的解集为A,若
的解集为A,若 ,求m的取值范围。(7分)
,求m的取值范围。(7分)
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南省长沙市田家炳实验中学高二(下)期末数学试卷(理科)(解析版) 题型:解答题
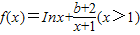 ,其中b为实数.
,其中b为实数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com