
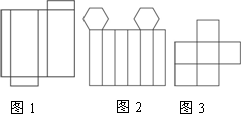
图1、图2、图3中的几个图形能否折叠成棱柱?请试折一下并回答为什么.
|
答案:图1可折成一个四棱柱;图2不能折成棱柱,因为折成后的几何体两底面在同一平面内;图3不能折成棱柱,因为与正方体的每个面相邻的面最多只有四个,因而展开后的图形中,任一个正方形在它的周围最多只应有四个正方形,而图中有一个正方形,在它的周围有5个正方形,这是不可能的. 思路解析:首先判断各图如果能折成棱柱则应该折成什么样的棱柱,再看各图与相应棱柱展开图有什么差异.这个题主要要求学生把握多面体的基本情况,运用纸张折叠,结合想象,掌握简单几何体的性质与构成. |
|
我们常见的多面体如棱柱、棱锥和棱台等,均可展开成平面图形,反之满足一定条件的平面图形亦可还原成空间多面体.在刚接触有关立体几何的内容时,一定要养成多动手、勤观察、善思考、好总结的良好习惯,为进一步学习立体几何的知识打下坚实的基础. |


科目:高中数学 来源:设计必修二数学苏教版 苏教版 题型:013
图1、图2、图3中的图形折叠后的图形分别是
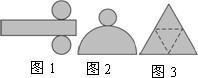
A.圆柱、圆锥、棱柱
B.圆柱、圆锥、棱锥
C.圆台、球棱锥
D.圆台、圆锥、棱柱
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com