
【题目】已知![]() ,
, ![]() .
.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)详见解析;(Ⅱ) ![]() .
.
【解析】试题分析:
(Ⅰ)由函数的解析式可得![]()
![]() ,当
,当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,由导函数的符号可知
时,由导函数的符号可知![]() 在
在![]() 单调递减;在
单调递减;在![]() 单调递增.
单调递增.
(Ⅱ)构造函数![]() ,问题转化为
,问题转化为![]() 在
在![]() 上恒成立,求导有
上恒成立,求导有![]() ,注意到
,注意到![]() .分类讨论:当
.分类讨论:当![]() 时,不满足题意. 当
时,不满足题意. 当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递增;所以
上单调递增;所以![]() ,满足题意.
,满足题意.
则实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(Ⅰ)![]()
![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() .∴
.∴![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,由
时,由![]() ,得
,得![]() .
.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以![]() 在
在![]() 单调递减;在
单调递减;在![]() 单调递增.
单调递增.
(Ⅱ)令![]() ,
,
问题转化为![]() 在
在![]() 上恒成立,
上恒成立,
![]() ,注意到
,注意到![]() .
.
当![]() 时,
时, ![]() ,
,
![]() ,
,
因为![]() ,所以
,所以![]() ,
, ![]() ,
,
所以存在![]() ,使
,使![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 递减,
递减,
所以![]() ,不满足题意.
,不满足题意.
当![]() 时,
时, ![]()
![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() ,
,
所以![]() ,
, ![]() 在
在![]() 上单调递增;所以
上单调递增;所以![]() ,满足题意.
,满足题意.
综上所述: ![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足a1=1,anan+1=2Sn , 设bn= ![]() ,若存在正整数p,q(p<q),使得b1 , bp , bq成等差数列,则p+q= .
,若存在正整数p,q(p<q),使得b1 , bp , bq成等差数列,则p+q= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图长方体![]() 中,
中,![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() 的中点
的中点

(1)求证:平面![]() 平面
平面![]() ;
;
(2)请在答题卡图形中画出直线![]() 与平面
与平面![]() 的交点
的交点![]() (保留必要的辅助线),写出画法并计算
(保留必要的辅助线),写出画法并计算![]() 的值(不必写出计算过程).
的值(不必写出计算过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年高考成绩揭晓,某高中再创辉煌,考后学校对于单科成绩逐个进行分析:现对甲、乙两个文科班的数学成绩进行分析,规定:大于等于135分为优秀,135分以下为非优秀,成绩统计后,得到如下的![]() 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为![]() .
.
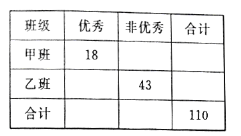
(1)请完成上面的列联表;
(2)请问:是否有75%的把握认为“数学成绩与所在的班级有关系”?
(3)用分层抽样的方法从甲、乙两个文科班的数学成绩优秀的学生中抽取5名学生进行调研,然后再从这5名学生中随机抽取2名学生进行谈话,求抽到的2名学生中至少有1名乙班学生的概率.
参考公式:![]() (其中
(其中![]() )
)
参考数据:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示.ABCD是等腰梯形,AB=20米,∠CBF=α(F在AB的延长线上,α为锐角).圆E与AD,BC都相切,且其半径长为100﹣80sinα米.EO是垂直于AB的一个立柱,则当sinα的值设计为多少时,立柱EO最矮? 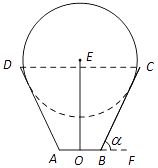
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·重庆高二检测)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=![]() AA1,D是棱AA1的中点.
AA1,D是棱AA1的中点.

(1)证明:平面BDC1⊥平面BDC.
(2)平面BDC1分此棱柱为两部分,求这两部分体积的比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com