练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】红铃虫是棉花的主要害虫之一，能对农作物造成严重伤害，每只红铃虫的平均产卵数y和平均温度x有关，现收集了以往某地的7组数据，得到下面的散点图及一些统计量的值.（表中）

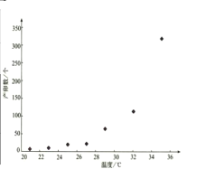
    平均温度

    21

    23

    25

    27

    29

    32

    35

    平均产卵数/个

    7

    11

    21

    24

    66

    115

    325

    27.429

    81.286

    3.612

    40.182

    147.714

    （1）根据散点图判断，与（其中自然对数的底数）哪一个更适宜作为平均产卵数y关于平均温度x的回归方程类型？（给出判断即可，不必说明理由）并由判断结果及表中数据，求出y关x的回归方程.（计算结果精确到小数点后第三位）

    （2）根据以往统计，该地每年平均温度达到28℃以上时红铃虫会造成严重伤害，需要人工防治，其他情况均不需要人工防治，记该地每年平均温度达到28℃以上的概率为.

    ①记该地今后5年中，恰好需要3次人工防治的概率为，求的最大值，并求出相应的概率p.

    ②当取最大值时，记该地今后5年中，需要人工防治的次数为X，求X的数学期望和方差.

    附：线性回归方程系数公式.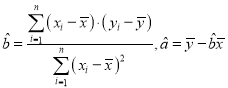

    【答案】（1）更适宜，；（2）①，；②，

    【解析】

    （1）根据散点图选择合适函数模拟，利用变量，构造线性回归方程，利用已知量求解出关于的线性回归方程，即可求解出y关于x的回归方程；

    （2）①先表示出，然后根据分析出的最大值以及的值；

    ②根据的值以及二项分布的均值与方差的计算方法求解出结果即可.

    解：（1）根据散点图可以判断，更适宜作为平均产卵数

    y关于平均温度x的回归方程类型；

    对两边取自然对数，得；

    令，得；

    因为，

    ；

    所以z关于x的回归方程为；

    所以y关于x的回归方程为；

    （2）（i）由，

    得，

    因为，令，得，解得；

    所以在上单调递增，在上单调递减，

    所以有唯一的极大值为，也是最大值；

    所以当时，；

    （ii）由（i）知，当取最大值时，，所以，

    所以X的数学期望为，

    方差为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】南宋数学家杨辉在《详解九章算法》和《算法通变本末》中，提出了一些新的垛积公式，所讨论的高阶等差数列与一般等差数列不同，前后两项之差并不相等，但是逐项差数之差或者高次差成等差数列对这类高阶等差数列的研究，在杨辉之后一般称为“垛积术”.现有高阶等差数列，其前7项分别为1，4，8，14，23，36，54，则该数列的第19项为（ ）（注：）

    A.1624B.1024C.1198D.1560

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|2x-1|+|x+m|．

    （l）当m=l时，解不等式f（x）≥3；

    （2）证明：对任意x∈R，2f（x）≥|m+1|-|m|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知非常数列满足，若，则( )

    A.存在，，对任意，，都有为等比数列

    B.存在，，对任意，，都有为等差数列

    C.存在，，对任意，，都有为等差数列

    D.存在，，对任意，，都有为等比数列

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在正四棱柱中，底面边长为，侧棱长为4，、分别为棱、的中点，；

    （1）求直线与平面所成角的大小；

    （2）求点到平面的距离；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩，其中有三个数据模糊.

    学生序号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    立定跳远（单位：米）

    1.96

    1.92

    1.82

    1.80

    1.78

    1.76

    1.74

    1.72

    1.68

    1.60

    30秒跳绳（单位：次）

    63

    a

    75

    60

    63

    72

    70

    a1

    b

    65

    在这10名学生中，进入立定跳远决赛的有8人，同时进入立定跳远决赛和30秒跳绳决赛的有6人，则

    （A）2号学生进入30秒跳绳决赛

    （B）5号学生进入30秒跳绳决赛

    （C）8号学生进入30秒跳绳决赛

    （D）9号学生进入30秒跳绳决赛

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知曲线的参数方程为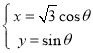（为参数），以为极点，轴的非负半轴为极轴建立极坐标系，曲线的极坐标方程为．

    （Ⅰ）求曲线的普通方程与曲线的直角坐标方程；

    （Ⅱ）设为曲线上的动点，求点到上点的距离的最小值，并求此时点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数.

    （1）讨论函数的单调性；

    （2）若，求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左顶点为，右焦点为，点在椭圆上．

    （1）求椭圆的方程；

    （2）若直线与椭圆交于两点，直线分别与轴交于点，在轴上，是否存在点，使得无论非零实数怎样变化，总有为直角？若存在，求出点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案