
设数列 的各项都是正数,且对任意
的各项都是正数,且对任意 ,都有
,都有 ,其中
,其中 为数列
为数列 的前
的前 项和。
项和。
(1)求证数列 是等差数列;
是等差数列;
(2)若数列 的前
的前 项和为Tn,求Tn。
项和为Tn,求Tn。
科目:高中数学 来源: 题型:解答题
大学生自主创业已成为当代潮流。长江学院大三学生夏某今年一月初向银行贷款20000元作开店资金,全部用作批发某种商品,银行贷款的年利率为6%,约定一年后一次还清贷款。已知夏某每月月底获得的利润是该月月初投人资金的15%,每月月底需要交纳个人所得税为该月所获利润的20%,当月房租等其他开支1500元,余款作为资金全部投入批发该商品再经营,如此继续,假定每月月底该商品能全部卖出。
(1)设夏某第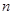 个月月底余
个月月底余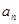 元,第
元,第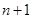 个月月底余
个月月底余 元,写出
元,写出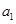 的值并建立
的值并建立 与
与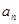 的递推关系式;
的递推关系式;
(2)预计年底夏某还清银行贷款后的纯收入。(参考数据:1.1211≈3.48,1.1212≈3.90,0.1211≈7.43×10﹣11,0.1212≈8.92×10﹣12)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设等比数列 的首项为
的首项为 ,公比为
,公比为 (
( 为正整数),且满足
为正整数),且满足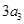 是
是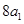 与
与 的等差中项;数列
的等差中项;数列 满足
满足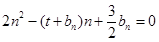 (
(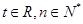 ).
).
(1)求数列 的通项公式;
的通项公式;
(2)试确定 的值,使得数列
的值,使得数列 为等差数列;
为等差数列;
(3)当 为等差数列时,对每个正整数
为等差数列时,对每个正整数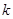 ,在
,在 与
与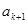 之间插入
之间插入 个2,得到一个新数列
个2,得到一个新数列 . 设
. 设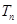 是数列
是数列 的前
的前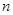 项和,试求满足
项和,试求满足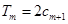 的所有正整数
的所有正整数 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com