
����Ŀ��ͨ�����ѯ��100�Ա�ͬ�Ĵ�ѧ���Ƿ�ij���˶����õ�����2��2��������
�� | Ů | �ܼ� | |
���� | 40 | ||
������ | 25 | ||
�ܼ� | 45 | 100 |
��1�������е�2��2����������������
��2���ܷ���99%�İ�����Ϊ�ϰ��ø����˶����Ա��йأ���˵�����ɣ�
����K2= ![]() ��
��
p��K2��k0�� | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
��3�����÷ֲ�����ķ��������ϰ��ø����˶��Ĵ�ѧ���г�ȡ6���齨�ˡ��˶������硱���ִӡ��˶������衱��ѡ��3�˲μ�ij��У����ս������ѡ��3���е�Ů��ѧ������ΪX����X�ķֲ��к���ѧ������
���𰸡�
��1���⣺ 2��2���������£�
�� | Ů | �ܼ� | |
���� | 40 | 20 | 60 |
������ | 15 | 25 | 40 |
�ܼ� | 55 | 45 | 100 |
��2���⣺K2= ![]() ��8.25��6.635��
��8.25��6.635��
��99%�İ�����Ϊ�ϰ��ø����˶����Ա��йأ�
��3���⣺�����⣬��ȡ6���У�����4����Ů��2����ѡ��3���е�Ů��ѧ������ΪX��X��ȡֵΪ0��1��2��
��P��X=0��= ![]() =
= ![]() ��P��X=1��=
��P��X=1��= ![]() =
= ![]() ��P��X=2��=
��P��X=2��= ![]() =
= ![]() ��
��
X�ķֲ���Ϊ
X | 0 | 1 | 2 |
P |
|
|
|
E��X��=0 ![]() ��+1��
��+1�� ![]() +2��
+2�� ![]() =1
=1
����������1������2��2���������ݹ��������пհײ������ݲ�����������2�����K2 �� ���ٽ�ֵ�Ƚϣ����ɵó����ۣ���3�������⣬��ȡ6���У�����4����Ů��2����ѡ��3���е�Ů��ѧ������ΪX��X��ȡֵΪ0��1��2���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�E��X����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ![]() �У�����
������![]() ����
����![]() �����������Ϊ
�����������Ϊ![]() ��
��![]() Ϊ��������������ԭ��
Ϊ��������������ԭ��![]() Ϊ���㣬
Ϊ���㣬![]() ��ķǸ�����Ϊ���ᣬ����������ϵ������
��ķǸ�����Ϊ���ᣬ����������ϵ������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ��
��
��1��������![]() ����ͨ���̺�����
����ͨ���̺�����![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
��2��������![]() ��
��![]() �ཻ��
�ཻ��![]() ��
��![]() ���㣬��
���㣬��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ڣ�0��+�ޣ��ϵĺ���f��x��������f��mn��=f��m��+f��n����m��n��0�����ҵ�x��1ʱ����f��x����0��
����֤��f�� ![]() ��=f��m����f��n����
��=f��m����f��n����
����֤��f��x���ڣ�0��+�ޣ�������������
�۱Ƚ�f�� ![]() ����
���� ![]() �Ĵ�С��
�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ����
����![]() ʱ������
ʱ������![]() ������
������
![]() ��a��ֵ��
��a��ֵ��
![]() �жϲ�֤������
�жϲ�֤������![]() �ĵ����ԣ�
�ĵ����ԣ�
![]() ��
��![]() ��
��![]() �ϵ�ֵ��
�ϵ�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|x��2|+|2x+a|��a��R��
��1����a=1ʱ���ⲻ��ʽf��x����5��
��2��������x0����f��x0��+|x0��2|��3����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������ҹ���������ˮƽ����ߣ����ֳ���ͨ��ҵ�õ�Ѹ�ͷ�չ��ij���������г���2017��ɽ��Ķ��ֳ�����ǰ��ʹ��ʱ�䣨���¼�ơ�ʹ��ʱ�䡱������ͳ�ƣ��õ�Ƶ�ʷֲ�ֱ��ͼ��ͼ1��


ͼ1 ͼ2
��1���ǡ���![]() ��ɽ��Ķ��ֳ������ѡȡһ�����ó���ʹ��������
��ɽ��Ķ��ֳ������ѡȡһ�����ó���ʹ��������![]() ��Ϊ�¼�
��Ϊ�¼�![]() ���Թ���
���Թ���![]() �ĸ��ʣ�
�ĸ��ʣ�
��2�����ݸ����������г�����ʷ���ϣ��õ�ɢ��ͼ��ͼ2������![]() (��λ����)��ʾ���ֳ���ʹ��ʱ�䣬
(��λ����)��ʾ���ֳ���ʹ��ʱ�䣬![]() (��λ����Ԫ)��ʾ��Ӧ�Ķ��ֳ���ƽ�����۸���ɢ��ͼ�������ɲ���
(��λ����Ԫ)��ʾ��Ӧ�Ķ��ֳ���ƽ�����۸���ɢ��ͼ�������ɲ���![]() ��Ϊ���ֳ�ƽ�����۸�
��Ϊ���ֳ�ƽ�����۸�![]() ������ʹ������
������ʹ������![]() �Ļع鷽�̣�����������±�������
�Ļع鷽�̣�����������±�������![]() ��
��![]() ����
����

�ٸ��ݻع鷽�����ͼ��������ݣ�����![]() ����
����![]() �Ļع鷽�̣�
�Ļع鷽�̣�
�ڸ����������г���ʹ��8������(��8��)�Ķ��ֳ���ȡ�ɽ��۸�![]() ��Ӷ�𣬶�ʹ��ʱ��8������(����8��)�Ķ��ֳ���ȡ�ɽ��۸�
��Ӷ�𣬶�ʹ��ʱ��8������(����8��)�Ķ��ֳ���ȡ�ɽ��۸�![]() ��Ӷ����ͼ1��ʹ��ʱ��ķ����У��Ը���������е�ֵ��������ĸ���ֵ������2017���������Ϊ�������ݣ���������������г��Գɽ���ÿ������ȡ��ƽ��Ӷ��
��Ӷ����ͼ1��ʹ��ʱ��ķ����У��Ը���������е�ֵ��������ĸ���ֵ������2017���������Ϊ�������ݣ���������������г��Գɽ���ÿ������ȡ��ƽ��Ӷ��
��ע���ٶ���һ������![]() ����ع�ֱ��
����ع�ֱ��![]() ��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ
��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ ��
��
�ڲο����ݣ�![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ��ij����Ϊ�˵������������ҹ����
��ij����Ϊ�˵������������ҹ����![]() ���������籭��̬�ȣ����ѡȡ��
���������籭��̬�ȣ����ѡȡ��![]() λ������е��飬������ͳ�����£�
λ������е��飬������ͳ�����£�
֧�� | ��֧�� | �ϼ� | |
�������� |
| ||
������ |
| ||
�ϼ� |
|
|
��1��������֪���ݣ��ѱ���������д������
��2�����ã�1����ɵı������ݻش��������⣺
��i���ܷ��ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ֧������������籭���Ա��йأ�
��ǰ������Ϊ֧������������籭���Ա��йأ�
��ii����֪�ڱ������֧������������籭��������������![]() λ�������ˣ�����
λ�������ˣ�����![]() λ�ǽ�ʦ���ִ���
λ�ǽ�ʦ���ִ���![]() λ���������������ȡ
λ���������������ȡ![]() �ˣ���������
�ˣ���������![]() λ��ʦ�ĸ���.
λ��ʦ�ĸ���.
����![]() ������
������![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ��Բ̨�У�AC���µ���ԲO��ֱ����EF���ϵ���ԲO���ֱ����FB��Բ̨��һ��ĸ�ߣ� 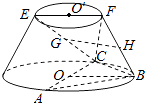
��1����֪G��H�ֱ�ΪEC��FB���е㣬��֤��GH��ƽ��ABC��
��2����֪EF=FB= ![]() AC=2
AC=2 ![]() ��AB=BC��������F��BC��A������ֵ��
��AB=BC��������F��BC��A������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�ԲC�ķ���Ϊ ![]() ����Ϊ��������������ԭ��OΪ���㣬x���������Ϊ���ᣬ����������ϵ����������ϵ��ȡ��ͬ�ĵ�λ���ȣ�ֱ��l�ļ����귽��Ϊ��cos��+��sin��=m��m��R����
����Ϊ��������������ԭ��OΪ���㣬x���������Ϊ���ᣬ����������ϵ����������ϵ��ȡ��ͬ�ĵ�λ���ȣ�ֱ��l�ļ����귽��Ϊ��cos��+��sin��=m��m��R����
��1����m=3ʱ���ж�ֱ��l��C��λ�ù�ϵ��
��2����C������ֻ��һ�㵽ֱ��l�ľ������ ![]() ʱ����C�ϵ�ֱ��l����Ϊ2
ʱ����C�ϵ�ֱ��l����Ϊ2 ![]() �ĵ�����꣮
�ĵ�����꣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com