
 =λ
=λ ,
, •i=0(其中0<λ<1,i为x轴上的单位向量),若|
•i=0(其中0<λ<1,i为x轴上的单位向量),若| |≤T(T为常数)在区间[m,n]上恒成立,则称y=f(x)在区间[m,n]上具有“T级线性逼近”.现有函数:①y=2x+1;②y=
|≤T(T为常数)在区间[m,n]上恒成立,则称y=f(x)在区间[m,n]上具有“T级线性逼近”.现有函数:①y=2x+1;②y= ;③y=x2.则在区间[1,2]上具有“
;③y=x2.则在区间[1,2]上具有“ 级 线性逼近”的函数的个数为( )
级 线性逼近”的函数的个数为( )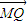 =λ
=λ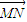 ,可得Q点在线段MN上,由
,可得Q点在线段MN上,由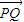 •
•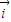 =0,可得P,Q两点的横坐标相等,故|
=0,可得P,Q两点的横坐标相等,故|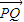 |即为P,Q两点纵坐标差的绝对值,分析三个函数中,x∈[1,2]时,|
|即为P,Q两点纵坐标差的绝对值,分析三个函数中,x∈[1,2]时,|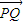 |≤
|≤ 是否恒成立,可得答案.
是否恒成立,可得答案.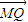 =λ
=λ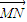 ,可得Q点在线段MN上,由
,可得Q点在线段MN上,由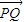 •
•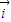 =0,可得P,Q两点的横坐标相等,故|
=0,可得P,Q两点的横坐标相等,故|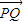 |即为P,Q两点纵坐标差的绝对值,
|即为P,Q两点纵坐标差的绝对值,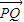 |=0≤
|=0≤ 恒成立,满足条件;
恒成立,满足条件;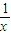 时,则M(1,1),N(2,
时,则M(1,1),N(2, ),线段MN的方程为y=-
),线段MN的方程为y=- x+
x+ ,此时|
,此时|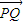 |=-
|=- x+
x+ -
-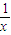 ,则|
,则|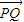 |′=-
|′=- +
+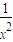 ,令|
,令|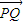 |′=0,则x=
|′=0,则x=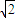 ,故当x=
,故当x=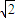 时,|
时,|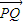 |取最大值
|取最大值 -
-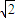 ,故|
,故|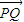 |≤
|≤ 恒成立,满足条件;
恒成立,满足条件;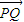 |=-x2+3x-2,当x=
|=-x2+3x-2,当x= 时,|
时,|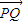 |取最大值
|取最大值 ,故|
,故|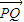 |≤
|≤ 恒成立,满足条件;
恒成立,满足条件; 级线性逼近”的函数的个数为3个
级线性逼近”的函数的个数为3个

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| MQ |
| MN |
| PQ |
| i |
| PQ |
| 1 |
| x |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:宁德模拟 题型:单选题
| MQ |
| MN |
| PQ |
| PQ |
| 1 |
| x |
| 1 |
| 4 |
| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com