
【题目】语文老师要从10篇课文中随机抽3篇让学生背诵,某学生只能背诵其中的6篇,求:
(1)抽到他能背诵的课文的数量的分布列;
(2)他能及格的概率.
【答案】
(1)解:随机抽出的3篇课文中该学生能背诵的篇数为X,则X是一个随机变量,它的可能取值为0,1,2,3,
且X服从超几何分布,
P(X=0)= ![]() =
= ![]() .P(X=1)=
.P(X=1)= ![]() =
= ![]() ,P(X=2)=
,P(X=2)= ![]() =
= ![]() ,P(X=3)=
,P(X=3)= ![]() =
= ![]() ,
,
∴X的分布列为:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
(2)解:该学生能及格表示他能背出2或3篇,
故他能及格的概率为P(X≥2)=P(X=2)+P(X=3)= ![]()
【解析】(1)随机抽出的3篇课文中该学生能背诵的篇数为X,则X是一个随机变量,它的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列.(2)该学生能及格表示他能背出2或3篇,由此能求出他能及格的概率.
【考点精析】本题主要考查了离散型随机变量及其分布列的相关知识点,需要掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】若定义在R上的函数![]() 对任意的
对任意的![]() ,都有
,都有![]() 成立,且当
成立,且当![]() 时,
时, ![]() .
.
(1)求![]() 的值;
的值;
(2)求证: ![]() 是R上的增函数;
是R上的增函数;
(3)若![]() ,不等式
,不等式![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是定义在R上的奇函数,且 ![]() 为偶函数,对于函数y=f(x)有下列几种描述,其中描述正确的是( ) ①y=f(x)是周期函数;②x=π是它的一条对称轴
为偶函数,对于函数y=f(x)有下列几种描述,其中描述正确的是( ) ①y=f(x)是周期函数;②x=π是它的一条对称轴
③(﹣π,0)是它图象的一个对称中心;④当 ![]() 时,它一定取最大值
时,它一定取最大值
A.①②
B.①③
C.②④
D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是偶函数,而y=f(x+1)是奇函数,且对任意0≤x≤1,都有f(x)≥0,f(x)是增函数,则a=f(2010),b=f( ![]() ),c=﹣f(
),c=﹣f( ![]() )的大小关系是( )
)的大小关系是( )
A.b<c<a
B.c<b<a
C.a<c<b
D.a<b<c
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AE:EB=1:2. 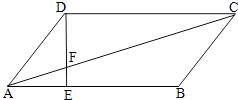
(1)求△AEF与△CDF的周长比;
(2)如果△AEF的面积等于6cm2 , 求△CDF的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列命题:
①命题:x∈(0,2),3x>x3的否定是:x∈(0,2),3x≤x3;
②若f(x)=2x﹣2﹣x,则x∈R,f(﹣x)=﹣f(x);
③若f(x)=x+![]() ,则x0∈(0,+∞),f(x0)=1;
,则x0∈(0,+∞),f(x0)=1;
④等差数列{an}的前n项和为Sn,若a4=3,则S7=21;
⑤在△ABC中,若A>B,则sinA>sinB.
其中真命题是____.(只填写序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com