
已知实数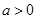 ,且
,且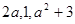 按某种顺序排列成等差数列.
按某种顺序排列成等差数列.
(1)求实数 的值;
的值;
(2)若等差数列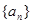 的首项和公差都为
的首项和公差都为 ,等比数列
,等比数列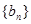 的首项和公比都为
的首项和公比都为 ,数列
,数列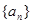 和
和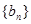 的前
的前 项和分别为
项和分别为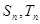 ,且
,且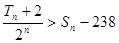 ,求满足条件的自然数
,求满足条件的自然数 的最大值.
的最大值.
(1)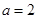 ;(2)14
;(2)14
解析试题分析:(1)由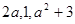 按某种顺序排列成等差数列,通过分类判断值的大小得到两类,再根据等差数列中项的性质,即可得到结论.
按某种顺序排列成等差数列,通过分类判断值的大小得到两类,再根据等差数列中项的性质,即可得到结论.
(2)由于等差数列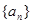 的首项和公差都为
的首项和公差都为 ,等比数列
,等比数列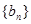 的首项和公比都为
的首项和公比都为 ,所以分别求出数列
,所以分别求出数列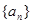 ,
,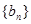 的通项公式.根据通项公式分别求出两个数列的前n项和的公式.再由
的通项公式.根据通项公式分别求出两个数列的前n项和的公式.再由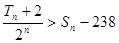 求出结论.
求出结论.
(3)解法一:由已知三个数有: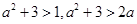 , 1分
, 1分
不妨设排列成递增的等差数列,则
①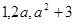 依次成等差数列,则有
依次成等差数列,则有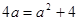 解得
解得 ,符合题意; 3分
,符合题意; 3分
②若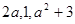 依次成等差数列,则有
依次成等差数列,则有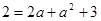 解得
解得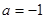 ,由
,由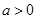 不符合题意; 5分
不符合题意; 5分
综上得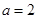 . 6分
. 6分
解法二:分三种情况讨论:
①若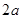 为等差中项,则有
为等差中项,则有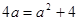 解得
解得 ,符合题意; 2分
,符合题意; 2分
②若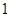 为等差中项,则有
为等差中项,则有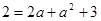 解得
解得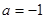 ,由
,由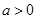 不符合题意; 4分
不符合题意; 4分
③若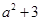 为等差中项,则有
为等差中项,则有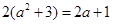 ,即
,即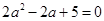 ,
, 方程无解; 6分
方程无解; 6分
综上得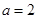 .
.
(2)解:由(1)知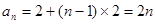 ,
,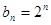 , 8分
, 8分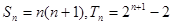 , 10分
, 10分
由已知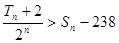 可得
可得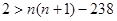 ,即
,即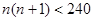 , 11分
, 11分
即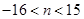 ,又
,又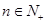 ,故
,故 的最大值为14. 12分
的最大值为14. 12分
考点:1.等差等比数列的通项公式.2.求和公式.3.不等式的交汇.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
(本题满分18分)本题共3个小题,第1小题满分3分,第2小题满分6分,第3小题满分9分.
已知数列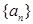 满足
满足 .
.
若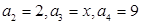 ,求
,求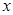 的取值范围;
的取值范围;
若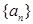 是公比为
是公比为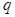 等比数列,
等比数列,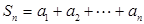 ,
,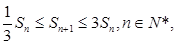 求
求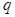 的取值范围;
的取值范围;
若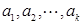 成等差数列,且
成等差数列,且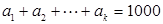 ,求正整数
,求正整数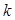 的最大值,以及
的最大值,以及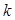 取最大值时相应数列
取最大值时相应数列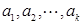 的公差.
的公差.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知{an}是正数组成的数列,a1=1,且点(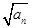 ,an+1)( n ∈N*)在函数y=x2+1的图象上.
,an+1)( n ∈N*)在函数y=x2+1的图象上.
(1)求数列{an}的通项公式;
(2)若数列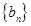 满足b1=1,
满足b1=1,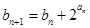 ,求证:
,求证: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列{an}满足an+1=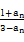 (n∈N*),且a1=
(n∈N*),且a1= .
.
(1)求证:数列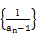 是等差数列,并求an.
是等差数列,并求an.
(2)令bn=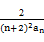 (n∈N*),求数列{bn}的前n项和Tn.
(n∈N*),求数列{bn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com