
����Ŀ��ij�ֳ���������![]() ��
�� ![]() �����ͺŵĻ�Ƥ����900�ֲָģ�
�����ͺŵĻ�Ƥ����900�ֲָģ� ![]() ��
�� ![]() ���ֳ�Ƥ���ػ����ֱ�Ϊ36�ֺ�60�֣����ֱ�Ϊ1.6��Ԫ/����2.4��Ԫ/�����ֳ�Ҫ���Ƥ����������21������
���ֳ�Ƥ���ػ����ֱ�Ϊ36�ֺ�60�֣����ֱ�Ϊ1.6��Ԫ/����2.4��Ԫ/�����ֳ�Ҫ���Ƥ����������21������![]() �ͳ�Ƥ������
�ͳ�Ƥ������![]() �ͳ�Ƥ7�����ֱ���
�ͳ�Ƥ7�����ֱ���![]() ��
�� ![]() ��ʾ����
��ʾ����![]() ��
�� ![]() ���ֳ�Ƥ�ĸ���.
���ֳ�Ƥ�ĸ���.
������![]() ��
�� ![]() �г�������������ѧ��ϵʽ����������Ӧ��ƽ������
�г�������������ѧ��ϵʽ����������Ӧ��ƽ������
���ֱ�����![]() ��
�� ![]() ���ֳ�Ƥ�ĸ����Ƕ���ʱ������ʹ��������٣����������С���.
���ֳ�Ƥ�ĸ����Ƕ���ʱ������ʹ��������٣����������С���.
���𰸡���������; ���ֱ�����![]() ��
��![]() ���ֳ�Ƥ5����12��ʱ�����С������С���Ϊ36.8��.
���ֳ�Ƥ5����12��ʱ�����С������С���Ϊ36.8��.
�����������������
��������֪�����г�![]() ��Լ���������ɻ���������
��Լ���������ɻ���������
�������Ŀ�꺯��Ϊ![]() ����ֱ��
����ֱ��![]() ����֪����ƽ��ֱ��
����֪����ƽ��ֱ��![]() ʱ��
ʱ�� ![]() ���Ӷ��ɵ����Ž⣮
���Ӷ��ɵ����Ž⣮
���������
��������֪![]() ��
�� ![]() �������ѧ��ϵʽΪ
�������ѧ��ϵʽΪ

�ö�Ԫһ�β���ʽ������ʾ��ƽ������Ϊͼ����Ӱ������ʾ.
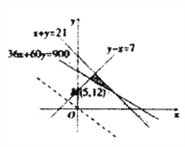
���������Ϊ![]() Ԫ����Ŀ�꺯��
Ԫ����Ŀ�꺯��![]() ������
������![]() ������б��Ϊ
������б��Ϊ![]() .��
.��![]() ���ϵĽؾ�Ϊ
���ϵĽؾ�Ϊ![]() ��һ��ƽ��ֱ��.
��һ��ƽ��ֱ��.
��![]() ȡ��Сֵʱ��
ȡ��Сֵʱ�� ![]() ��ֵ��С������Ϊ
��ֵ��С������Ϊ![]() ��
�� ![]() ����Լ��������������ͼ��֪����ֱ��
����Լ��������������ͼ��֪����ֱ��![]() �����������еĵ�
�����������еĵ�![]() ʱ���ؾ�
ʱ���ؾ�![]() ��ֵ��С����
��ֵ��С����![]() ��ֵ��С.
��ֵ��С.
�ⷽ����![]() ���õ�
���õ�![]() ������Ϊ
������Ϊ![]() .
.
����![]() ����Ԫ��.
����Ԫ��.
�𣺷ֱ�����![]() ��
��![]() ���ֳ�Ƥ5����12��ʱ�����С������С���Ϊ36.8��.
���ֳ�Ƥ5����12��ʱ�����С������С���Ϊ36.8��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=2 ![]() ��
��
��1������f��x���Ķ������ֵ��
��2������f��x���ĵ������䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
����������![]() ��
��![]() ��������
��������![]() ��ֱ��
��ֱ��![]() ��ֱ����
��ֱ����![]() ��ֵ��
��ֵ��
����![]() ʱ����֤������ʵ��
ʱ����֤������ʵ��![]() ʹ
ʹ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() .
.
������![]() ������
������![]() ��
��![]() �ĵ������䣻
�ĵ������䣻
������![]() ��3����ͬ��ʵ������ʵ��
��3����ͬ��ʵ������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
����![]() ʱ�������������
ʱ�������������![]() ��������
��������![]() ��ʹ��
��ʹ��![]() ��������������������
��������������������![]() ��ȡֵ�ļ���.
��ȡֵ�ļ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���˻����������ļֽṹ����ͼ��ͼ��ʾ��������Ȧ�ĸֹǼ�����������ͬ����Բ�����dz���������Բ���ơ�
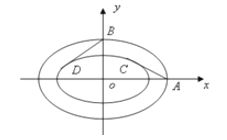
��1����֪��Բ![]() ��д������Բ
��д������Բ![]() �����ҽ�����
�����ҽ�����![]() ���ϡ��̰��᳤Ϊ
���ϡ��̰��᳤Ϊ![]() ����Բ
����Բ![]() �ı����̣�������Բ
�ı����̣�������Բ![]() �ϴ�������
�ϴ�������![]() ��
��![]() ����ֱ��
����ֱ��![]() �Գƣ���ʵ��
�Գƣ���ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2���������Բ����A��B���ڲ���Բ������AC��BD�����ڲ���Բ����Ϊ![]() +
+![]() =1 (a
=1 (a![]() b
b![]() 0)��AC��BD��б��֮��Ϊ��
0)��AC��BD��б��֮��Ϊ��![]() ������Բ�������ʡ�
������Բ�������ʡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=cos4x��sin4x�����н�����ȷ���ǣ� ��
A.����f��x��������[0�� ![]() ]���Ǽ�����
]���Ǽ�����
B.����f��x����ͼ�����ԭ��Գ�
C.f��x������С������Ϊ ![]()
D.f��x����ֵ��Ϊ[�� ![]() ��
�� ![]() ]
]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲC�İ뾶Ϊ2��Բ����![]() ����������ϣ�ֱ��
����������ϣ�ֱ��![]() ��ԲC����.
��ԲC����.
��1����ԲC�ķ��̣�
��2������![]() ��ֱ��
��ֱ��![]() ��ԲC���ڲ�ͬ������
��ԲC���ڲ�ͬ������![]() ���ҵ�
���ҵ�![]() ʱ����
ʱ����![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲC��Բ����ֱ����![]() ������ֱ��
������ֱ��![]() �����ڵ�
�����ڵ�![]()
��1����ԲC�ķ��̣�
��2���Ƿ���ڹ���![]() ��ֱ��
��ֱ��![]() ��ԲC����
��ԲC����![]() ���㣬��
���㣬��![]() �����Ϊ
�����Ϊ![]() ��OΪ����ԭ�㣩�������ڣ����ֱ��
��OΪ����ԭ�㣩�������ڣ����ֱ��![]() �ķ��̣��������ڣ���˵������.
�ķ��̣��������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������� ![]() �У�����
�У�����![]() �Ͳ���
�Ͳ���![]() ���Ǿ��Σ�
���Ǿ��Σ� ![]() �DZ߳�Ϊ
�DZ߳�Ϊ![]() ���������Σ�
���������Σ� ![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ���е�.
���е�.
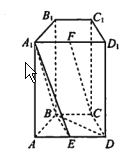
��1����֤�� ![]() ƽ��
ƽ��![]() ��
��
��2����֤��ƽ��![]() ƽ��
ƽ��![]() .
.
��3����![]() ƽ��
ƽ��![]() ������
������![]() �ij���.
�ij���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com