
【题目】已知抛物线![]() 的焦点曲线
的焦点曲线![]() 的一个焦点,
的一个焦点, ![]() 为坐标原点,点
为坐标原点,点![]() 为抛物线
为抛物线![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 轴的平行线交抛物线的准线于
轴的平行线交抛物线的准线于![]() ,直线
,直线![]() 交抛物线于点
交抛物线于点![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)求证:直线![]() 过定点
过定点![]() ,并求出此定点的坐标.
,并求出此定点的坐标.
【答案】(I)![]() ;(II)证明见解析.
;(II)证明见解析.
【解析】试题分析:(Ⅰ)将曲线![]() 化为标准方程,可求得
化为标准方程,可求得![]() 的焦点坐标分别为
的焦点坐标分别为![]() ,可得
,可得![]() ,所以
,所以![]() ,即抛物线的方程为
,即抛物线的方程为![]() ;(Ⅱ)结合(Ⅰ),可设
;(Ⅱ)结合(Ⅰ),可设![]() ,得
,得 ,从而直线
,从而直线![]() 的方程为
的方程为![]() ,联立直线与抛物线方程得
,联立直线与抛物线方程得![]() ,解得
,解得![]() ,直线
,直线![]() 的方程为
的方程为 ,整理得
,整理得![]() 的方程为
的方程为![]() ,此时直线恒过定点
,此时直线恒过定点![]() .
.
试题解析:(Ⅰ)由曲线![]() ,化为标准方程可得
,化为标准方程可得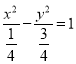 , 所以曲线
, 所以曲线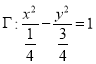 是焦点在
是焦点在![]() 轴上的双曲线,其中
轴上的双曲线,其中![]() ,故
,故![]() ,
, ![]() 的焦点坐标分别为
的焦点坐标分别为![]() ,因为抛物线的焦点坐标为
,因为抛物线的焦点坐标为![]() ,由题意知
,由题意知![]() ,所以
,所以![]() ,即抛物线的方程为
,即抛物线的方程为![]() .
.
(Ⅱ)由(Ⅰ)知抛物线![]() 的准线方程为
的准线方程为![]() ,设
,设![]() ,显然
,显然![]() .故
.故 ,从而直线
,从而直线![]() 的方程为
的方程为![]() ,联立直线与抛物线方程得
,联立直线与抛物线方程得![]() ,解得
,解得![]()
①当![]() ,即
,即![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,
,
②当![]() ,即
,即![]() 时,直线
时,直线![]() 的方程为
的方程为 ,整理得
,整理得![]() 的方程为
的方程为![]() ,此时直线恒过定点
,此时直线恒过定点![]() ,
, ![]() 也在直线
也在直线![]() 的方程为
的方程为![]() 上,故直线
上,故直线![]() 的方程恒过定点
的方程恒过定点![]() .
.
【题型】解答题
【结束】
21
【题目】已知函数![]() ,
, ![]()
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)若![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若数列![]() 满足
满足![]() ,
, ![]() ,记
,记![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() .
.
【答案】(I)![]() ;(II)
;(II)![]() ;(III)证明见解析.
;(III)证明见解析.
【解析】试题分析:(Ⅰ)求出![]() ,在定义域内,分别令
,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间, ![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(Ⅱ)当
的减区间;(Ⅱ)当![]() 时,因为
时,因为![]() ,所以
,所以![]() 显然不成立,先证明因此
显然不成立,先证明因此![]() 时,
时, ![]() 在
在![]() 上恒成立,再证明当
上恒成立,再证明当![]() 时不满足题意,从而可得结果;(III)先求出等差数列的前
时不满足题意,从而可得结果;(III)先求出等差数列的前![]() 项和为
项和为![]() ,结合(II)可得
,结合(II)可得![]() ,各式相加即可得结论.
,各式相加即可得结论.
试题解析:(Ⅰ)由![]() ,得
,得![]() .所以
.所以![]()
令![]() ,解得
,解得![]() 或
或![]() (舍去),所以函数
(舍去),所以函数![]() 的单调递减区间为
的单调递减区间为 ![]() .
.
(Ⅱ)由![]() 得,
得, ![]()
当![]() 时,因为
时,因为![]() ,所以
,所以![]() 显然不成立,因此
显然不成立,因此![]() .
.
令![]() ,则
,则 ,令
,令![]() ,得
,得![]() .
.
当![]() 时,
时, ![]() ,
, ![]() ,∴
,∴![]() ,所以
,所以![]() ,即有
,即有![]() .
.
因此![]() 时,
时, ![]() 在
在![]() 上恒成立.
上恒成立.
②当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
∴![]() ,不满足题意.
,不满足题意.
综上,不等式![]() 在
在![]() 上恒成立时,实数
上恒成立时,实数![]() 的取值范围是
的取值范围是![]() .
.
(III)证明:由![]() 知数列
知数列![]() 是
是![]() 的等差数列,所以
的等差数列,所以![]()
所以![]()
由(Ⅱ)得, ![]() 在
在![]() 上恒成立.
上恒成立.
所以![]() . 将以上各式左右两边分别相加,得
. 将以上各式左右两边分别相加,得
![]() .因为
.因为![]()
所以![]()
所以![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】我们称一个非负整数集合![]() (非空)为好集合,若对任意
(非空)为好集合,若对任意![]() ,或者
,或者![]() ,或者
,或者![]() .以下记
.以下记![]() 为
为![]() 的元素个数.
的元素个数.
(Ⅰ)给出所有的元素均小于![]() 的好集合;(给出结论即可)
的好集合;(给出结论即可)
(Ⅱ)求出所有满足![]() 的好集合;(同时说明理由)
的好集合;(同时说明理由)
(Ⅲ)若好集合![]() 满足
满足![]() ,求证:
,求证: ![]() 中存在元素
中存在元素![]() ,使得
,使得![]() 中所有元素均为
中所有元素均为![]() 的整数倍.
的整数倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() 与常数
与常数![]() ,若
,若![]() 恒成立,则称
恒成立,则称![]() 为函数
为函数![]() 的一个“
的一个“![]() 数对”;设函数
数对”;设函数![]() 的定义域为
的定义域为![]() ,且
,且![]() .
.
(Ⅰ)若![]() 是
是![]() 的一个“
的一个“![]() 数对”,且
数对”,且![]() ,求常数
,求常数![]() 的值;
的值;
(Ⅱ)若![]() 是
是![]() 的一个“
的一个“![]() 数对”,求
数对”,求![]() ;
;
(Ⅲ)若![]() 是
是![]() 的一个“
的一个“![]() 数对”,且当
数对”,且当![]() ,
, ![]() ,求
,求![]() 的值及
的值及![]() 在区间
在区间![]() 上的最大值与最小值.
上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() )的图象与
)的图象与![]() 轴的交点中,相邻两个交点之间的距离为
轴的交点中,相邻两个交点之间的距离为![]() ,且图象上一个最高点为
,且图象上一个最高点为![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)先把函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度,然后再把所得图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数
个单位长度,然后再把所得图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() 的图象,试写出函数
的图象,试写出函数![]() 的解析式.
的解析式.
(3)在(2)的条件下,若存在![]() ,使得不等式
,使得不等式![]() 成立,求实数
成立,求实数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 是半圆
是半圆![]() 的直径,
的直径,![]() ,
,![]() 是将半圆圆周四等分的三个分点.
是将半圆圆周四等分的三个分点.

(1)从![]() 这5个点中任取3个点,求这3个点组成直角三角形的概率;
这5个点中任取3个点,求这3个点组成直角三角形的概率;
(2)在半圆内任取一点![]() ,求
,求![]() 的面积大于
的面积大于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年初,湖北出现由新型冠状病毒引发的肺炎.各级政府相继启动重大突发公共卫生事件一级响应,全国齐心抗击疫情,基本上控制住了疫情.下图为
年初,湖北出现由新型冠状病毒引发的肺炎.各级政府相继启动重大突发公共卫生事件一级响应,全国齐心抗击疫情,基本上控制住了疫情.下图为![]() 月
月![]() 日至
日至![]() 月
月![]() 日我国新型冠状病毒肺炎全国总新增确诊人数和新增境外输入确诊人数趋势图(数据来源:国家卫健委官网),则下列表述中错误的是( )
日我国新型冠状病毒肺炎全国总新增确诊人数和新增境外输入确诊人数趋势图(数据来源:国家卫健委官网),则下列表述中错误的是( )

A.3月上旬全国总新增确诊人数呈波动下降趋势.
B.3月中下旬全国总新增确诊人数开始反弹的主要原因是境外输入病例的增加.
C.全国总新增确诊人数随着境外输入确诊人数变化而变化.
D.4月中下旬国内新增确诊人数呈越来越少的趋势.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com