
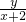 的取值范围;
的取值范围;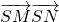 的最小值.
的最小值. 解:(1)已知两定点A(-2,0),B(1,0),如果动点P满足|PA|=2|PB|,设P点的坐标为(x,y),
解:(1)已知两定点A(-2,0),B(1,0),如果动点P满足|PA|=2|PB|,设P点的坐标为(x,y), 表示P(x,y)与定点(-2,0)所连直线的斜率
表示P(x,y)与定点(-2,0)所连直线的斜率 即y=k(x+2),即kx-y+2k=0,圆心(2,0)到此直线的距离为:
即y=k(x+2),即kx-y+2k=0,圆心(2,0)到此直线的距离为: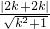 ,令d=2得
,令d=2得 ?k=±
?k=± ,
,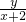 的取值范围为[-
的取值范围为[- ,
, ].
]. )2=22+(0-
)2=22+(0- )2即x2+y2-ty-4=0,又(x-2)2+y2=4
)2即x2+y2-ty-4=0,又(x-2)2+y2=4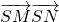 =
=
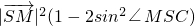

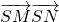 =m2+
=m2+ -12,此函数在m≥4时是单调增函数,
-12,此函数在m≥4时是单调增函数, -12=42+
-12=42+ -12=6.
-12=6.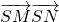 的最小值6.
的最小值6.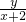 的几何意义,转化为P(x,y)与定点(-2,0)所连直线的斜率,故易求.
的几何意义,转化为P(x,y)与定点(-2,0)所连直线的斜率,故易求.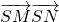 =
= =
=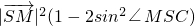 =
=
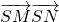 =m2+
=m2+ +4,此函数在m≥4时是单调增函数,从而求出
+4,此函数在m≥4时是单调增函数,从而求出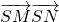 的最小值.
的最小值.

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| y2 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| y |
| x+2 |
| SM |
| SN |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com