若在所给条件下,数列{an}的每一项的值都能唯一确定,则称该数列是“确定的”,在下列各组条件下,有哪些数列是“确定的”?请把对应的序号填在横线上 .
(注:Sn是{an}的前n项和,n∈N*)
①{an}是等差数列,S1=2,S2=3;
②{an}是等差数列,S1=1,S5=25;
③{an}是等比数列,S1=1,S4=31;
④{an}是等比数列,S1=2,a3=2;
⑤{an}满足Sn=2an.
【答案】
分析:通过题目提供的信息,由等差数列,等比数列的项和前n项和以及它们的关系求得其通项,即可确定该数列中的项,从而得到答案.
解答:解:∵①{a
n}是等差数列,设其公差为d,
又∵S
1=2,S
2=3∴a
2=3-2=1∴d=1-2=-1∴a
n=2-(n-1)=3-n 每一项都是确定的,∴①对
∵②{a
n}是等差数列,S
1=1,S
5=25∴S
5=
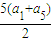
=
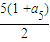
=25∴a
5=9∴4d=9-1=8∴d=2∴a
n=1+2(n-1)=2n-1∴②对
∵③{a
n}是等比数列,S
1=1,S
4=31 设其公比为q(q≠1),∴S
4=
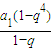
=
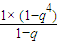
=31∴q
3+q
2+q=30
令y=q
3+q
2+q,则y′=3q
2+2q+1,∵其△=4-12=-8<0∴y′>0恒成立∴函数y=q
3+q
2+q为单调增函数,
∴方程q
3+q
2+q=30有唯一的解,即{a
n}的每一项都是确定的.∴③对.
④{a
n}是等比数列,S
1=2,a
3=a
1•q
2=2∴q
2=1∴q=±1∴{a
n}的各项是不确定的∴④不对.
⑤{a
n}满足S
n=2a
n∴a
1=2a
1∴a
1=0 当n≥2时,a
n=S
n-S
n-1=2a
n-2a
n-1 ∴a
n=2a
n-1,∴a
n=0.∴⑤对
故答案为:①②③⑤
点评:本题是一道信息给予题,正确把握新概念是解决问题的根本,主要考查了等差,等比关系的确定,是个基础题.

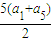 =
=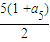 =25∴a5=9∴4d=9-1=8∴d=2∴an=1+2(n-1)=2n-1∴②对
=25∴a5=9∴4d=9-1=8∴d=2∴an=1+2(n-1)=2n-1∴②对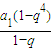 =
=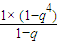 =31∴q3+q2+q=30
=31∴q3+q2+q=30
